
Lorsque l’on voit le Soleil se lever ou se coucher, on a tendance à dire que le Soleil tourne autour de la Terre. Et en un sens, c’est vrai : vu depuis la Terre, dans le référentiel terrestre, le Soleil tourne autour de la Terre. Si maintenant on se place dans le référentiel solaire, la Terre tourne sur elle-même (et autour du Soleil aussi).
Alors quelle est la situation qui représente le mieux la réalité ?
Quand on a 5 ans, ou bien si l’on vit durant l’antiquité, alors on n’a pas encore la science ou les instruments adéquats pour répondre à sur cette question de façon juste. Il n’est donc pas absurde de croire ce que l’on voit, c’est à dire que le Soleil tourne autour de la Terre.
Mais ceci a changé lorsque Galilée inventa le télescope, et qu’il eut l’idée de pointer son instrument vers le ciel nocturne. C’est alors qu’il vit — entre autres choses — les lunes de Jupiter tourner autour de lui en décrivant des cercles.
Galilée comprit alors sur la Terre, comme toutes les planètes doivent décrire des cercles autour du Soleil : en effet, il n’y a que dans cette configuration que les astres ont des orbites circulaires (depuis la Terre, la trajectoire des planètes Mars, Mercure du Vénus sont étranges : elles avancent, reculent, ralentissent, bref font n’importe quoi).
Il vit aussi que les planètes tournent sur elles-mêmes.
Il comprit alors que tout ceci devait aussi s’appliquer à la Terre, mais comment le prouver ?
Comment prouver que la Terre tourne sur elle-même ?
De la déviation des pendules
Proposer une preuve pour la rotation de la planète n’est pas simple quand on est coincé sur ladite planète et qu’on tourne avec elle : en effet, on ne la sent pas tourner. Pour nous, elle semble donc immobile.
Il existe pourtant une méthode, et elle est apparue en 1851, grâce à Léon Foucault.
Léon Foucault remarqua qu’un pendule oscillant assez longtemps voyait son axe dévier au fil des heures. Cette observation datait de 1660, mais l’origine en demeurait jusqu’alors toujours inconnue :
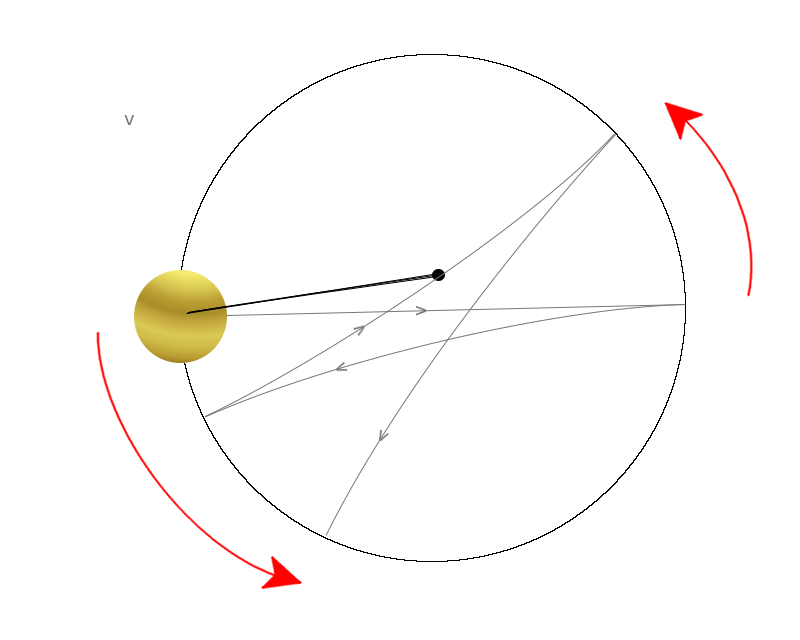
Foucault y voyait là la conséquence de la rotation de la Terre, et il entendait bien le prouver !
L’effet de Coriolis
Imaginez-vous être sur un manège en rotation lente. De votre point de vue, le manège est immobile et le reste du monde tourne.
Maintenant, vous sortez de votre poche une balle et vous l’envoyez devant vous sur le manège : la balle est déviée !
Comment expliquer ça ?
En fait, la balle réagit principalement à son inertie, c’est à dire l’impulsion de départ que vous lui donnez. Comme elle est ronde, elle peut rouler où elle veut et le manège n’a que peu d’effet dessus. Le principe d’inertie dit qu’un objet qui se déplace va toujours en ligne droite tant qu’il ne rencontre pas de force opposé. Et c’est ce que la balle fait : elle va en ligne droite, indépendamment du manège. Vu du manège en rotation, la balle — tout comme le décor — effectue une rotation :
Cette effet est appelé « effet de Coriolis ».
Il apparaît quand on observe un objet en déplacement rectiligne depuis dans un référentiel en rotation.
Tout comme depuis le manège on voit le reste du monde tourner, on verra aussi la balle faire un virage, alors qu’en vrai ni le monde tourne, ni la balle ne vire. C’est le manège qui tourne. Mais ça, si on est dessus en rotation également, on ‘e le sait pas forcément.
Ce qu’il faut bien voir ici, c’est qu’aucune force n’agit sur la balle : il n’y a pas de ficelle ni de pente qui la pousserait à faire une trajectoire circulaire. L’effet de cercle est uniquement dû au fait que le manège et ses observateurs sont en rotation.
L’absence de force concrète me pousse d’ailleurs à employer le terme de « effet de Coriolis » comme en anglais, plutôt que « force de Coriolis ».
Prouver que la Terre tourne
Avec la manège ci-dessus, on a montré qu’un référentiel en rotation semble dévier les objets. Mais si l’on sait que c’est le référentiel qui tourne, on comprend que l’objet n’est pas dévié : il semble seulement l’être.
L’idée de Léon Foucault est alors de raisonner en sens inverse : il voit que les pendules sont déviés sans qu’on n’y applique une quelconque force. Il en déduit donc que c’est le référentiel dans lequel ils se trouvent qui est en rotation. Et le référentiel, ici, est celui de la Terre !
Le pendule oscille donc normalement et c’est le référentiel terrestre qui tourne :
Il y a meme encore plus solide comme preuve. La déviation des pendules dépend de la latitude à laquelle on se trouve. Elle est nulle à l’équateur, et maximale au niveau des pôles.
Bien-sûr, il est déjà montré que la Terre est ronde (la circonférence de la Terre est connue depuis plus de 2 200 ans).
L’effet de Coriolis n’est pas la même si on est sur le pôle avec la surface perpendiculaire à l’axe de rotation, ou à l’équateur avec la surface parallèle à l’axe de rotation.
Au Panthéon à Paris, de latitude 48°52', le pendule est constamment dévié vers l’est, et cette déviation effectue un tour complet en environ 31 heures et 47 minutes (11°47' par heure). On appelle ça la durée du jour pendulaire.
Au pôles, le jour pendulaire est égal au jour sidéral (et la rotation du pendule est maximale). À l’équateur, le jour pendulaire est infini (sa rotation est nulle).
Entre les deux, on observe un effet intermédiaire : le jour pendulaire $J_p$ dépend de la latitude selon la relation :
$$J_p = \frac{J_s}{\sin(\theta)}$$
Où :
- $J_p$ est le jour pendulaire, donc la période de rotation de l’axe du pendule ;
- $J_s$ la durée d’un jour sidéral (la durée d’une rotation de la Terre) : 23 h 56 min pour la Terre (soit 84 164 secondes) ;
- $\theta$ (théta) est la latitude, un angle : variant de 0° à l’équateur à 90° au pôle Nord.
On retrouve ces résultats avec la démonstration mathématique, qui explique exactement ce que l’on observe, et il a donc été montré l’origine de la déviation des pendules comme étant la rotation de la Terre. Ceci constitue donc une preuve directe de la rotation de la Terre sur elle-même (et aussi, indirectement, qu’elle est ronde, bien que ce ne fut plus à démontrer).
L’explication de Foucault permet d’expliquer précisément la déviation des pendules, observée depuis des siècles. Ces observations sont expliquées très précisément avec l’hypothèse d’une rotation de la Terre, hypothèse dès lors validée.
Depuis, on peut venir « voir la Terre tourner » un peu partout dans le monde : des pendules de Foucault sont installés dans tous les grands musées.
Le pendule original que Foucault utilisa était une boule de laiton de 28 kg suspendue à un câble de 67 mètres, au toit du Panthéon, à Paris.
De telles dimensions sont en effet nécessaires pour faire en sorte que le pendule oscille durant plusieurs heures, le temps nécessaire pour que la déviation soit perceptible.