
Suite à mon article sur les dérivées, vous avez été plusieurs à me demander un article sur les intégrales. Le voici.
Si vous n’avez pas lu mon article sur les dérivées, je vous conseille de le lire : à défaut de vous réapprendre des choses que savez sûrement déjà, ils vous familiarisera avec ma méthode d’explication.
Représenter une fonction
J’explique ce qu’est une fonction en mathématiques dans mon article sur les dérivées. Ici, je reprends très brièvement comment on fait pour représenter une fonction.
Reprenons notre exemple de fonction :
$$g(x)=-3x^3+5x^2+5$$
La fonction $g$ permet en partant d’un nombre $x$ d’associer un autre nombre $g(x)$. Si on donne la valeur $1$ à $x$, alors la fonction lui associe le nombre $-3 \times 1^3+5 \times 1^2+5$ soit $7$.
En appliquant la fonction à tous les nombres possibles, et en plaçant chaque couple de nombre ainsi obtenu dans un repère, avec $x$ en abscisse et $g(x)$ en ordonnée, on obtient une courbe représentative de la fonction :

Maintenant, tout comme la dérivée constitue en fait l’inclinaison de la courbe (ou la variation de la fonction) en un point donné, on peut remarquer d’autres choses sur la courbe d’une fonction.
Par exemple, quelle est la surface située entre la courbe et l’axe des abscisses ?
Je parle de cette surface là :
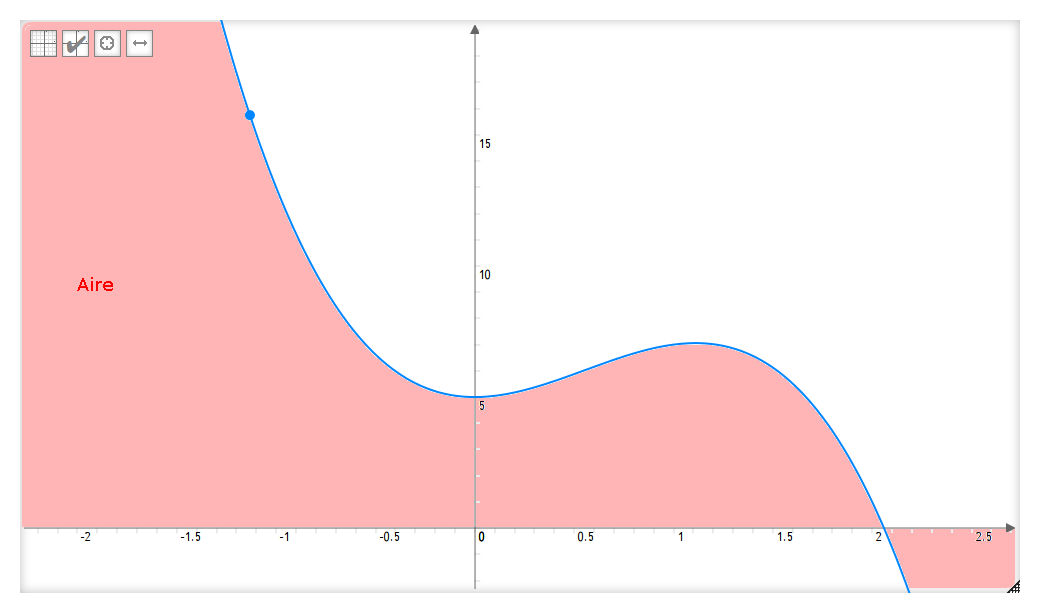
Ici, la surface en rose correspond à l’aire sous la courbe entre les bornes −2,5 et +2,6 (certaines parties sont coupées). Et bien mathématiquement, cette aire est égale à l’intégrale de la fonction $g$ sur l’interval [−2,5;2,6].
Une intégrale correspond donc à une aire située sous la courbe.
Un exemple de calcul d’intégral entre deux bornes à partir d’une aire sous une fonction constante
L’aire en rose pour la fonction $g$ n’est pas facile à mesurer : la courbe n’est pas une forme géométrique.
Prenons quelque chose de plus simple, comme une fonction constante : $f(x) = 3$ :

Calculons l’aire sous la courbe entre les points −2 et +2. Ça correspond donc à cette aire :

Combien mesure cette aire ?
Ici, la surface est très simple à calculer : c’est un rectangle. La hauteur du rectangle est de 3 et la largeur va de −2 à +2, donc mesure 4. L’aire sous la courbe, entre ces deux bornes est donc 12 cm².
Intégral complète d’une fonction
L’aire entre deux bornes c’est bien mais on peut faire mieux : on peut chercher l’aire sous la courbe sur tout le domaine de définition de la fonction.
Pour la fonction $f(x)$, l’aire sous toute la courbe est donc toujours un rectangle. La hauteur du rectangle est toujours 3. Sa largeur, même si elle est infinie (si la fonction va de $-\infty$ à $+\infty$), correspond en fait à la largeur sur l’axe des $x$ : c’est donc tout simplement $x$.
Pour une fonction $f(x) = 3$, l’aire sous la courbe est donc égale à $3\times x$.
La fonction qui donne l’aire sous la courbe d’une autre fonction est nommé la fonction « primitive ». Elle se note généralement avec une lettre capitale. La primitive de la fonction $f$ se nomme donc $F$.
On a donc $F(x) = 3\times x$.
On remarque que la dérivée de $F$ correspond à $f$ : la primitive est l’inverse de la dérivée.
Si vous savez vu les intégrales en cours, vous avez effectivement dû voir que la primitive d’une fonction constante, c’est une fonction linéaire. On retrouve donc bien cette propriété ici.
Un exemple de calcul d’intégral à partir d’une aire sous une fonction linéaire
Bon, une fonction constante, c’est simple. Passons à une fonction linéaire. Prenons la fonction $h(x) = 3\times x$, et calculons l’aire sous la courbe :

On voit ici que l’aire du côté droite de l’axe des ordonnées correspond à un triangle rectangle. L’aire d’un triangle rectangle est égal à la moitié de l’aire du rectangle dont il est issu.
Les côtés du triangle à prendre en compte sont les deux côtés horizontal et vertical du triangle : il correspondent respectivement à la distance à l’origine, donc à $x$ ; et à l’ordonnée. Or, pour un point $x$, l’ordonnée correspond à la $h(x)$, soit $3 \times x$.
L’aire du triangle de droite sur le graphique correspond donc à la moitié de $3\times x\times x$, soit $\frac{3}{2}x^2$.
Le même raisonnement est appliqué sur le triangle de gauche sur la graphique, celui pour les $x$ négatifs. On obtient bien-sûr le même résultat (en valeur absolue). Au final, on obtient donc la valeur de l’intégrale sur tout le domaine de définition de la fonction $h$.
Cette aire est calculée par la fonction primitive $H$ et qui vaut donc $\frac{3}{2}x^2$. N’est-ce pas là non plus l’expression de la primitive de la fonction linéaire $h(x)$ telle qu’apprise en cours ?
Le calcul d’intégral pour une fonction quelconque
Bon, on vient de revérifier les formules pour les intégrales des fonctions constantes et linéaires. Mais pour une fonction quelconque, comme la fonction $g$ du début ?
Ici, c’est bien plus dur à redémontrer graphiquement : les courbes ne constituent pas de formes géométriques.
On peut cependant approcher l’aire de la courbe avec des rectangles :
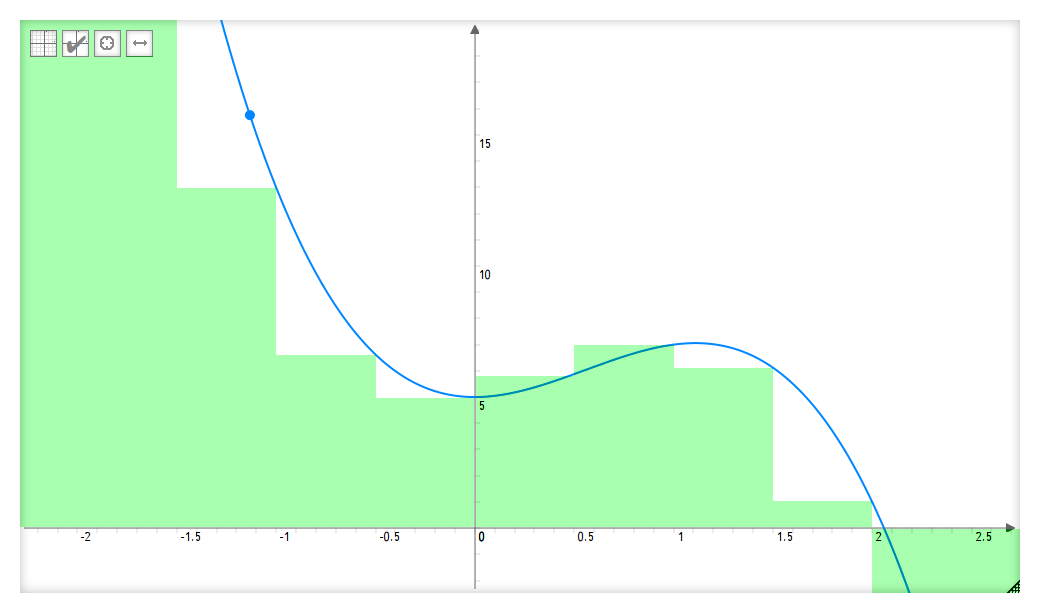
On voit que l’aire de tous les rectangles additionnée approche à peu près la courbe. Ici, j’ai pris des rectangles tous les 0,5 cm, et la hauteur du rectangle s’arrête quand son côté droit atteint la courbe. L’aire d’un rectangle est donc : $g(n \times 0,5)\times 0,5$, où $n$ est un entier qui correspond au rectangle choisi (n=3 correspond au 3e triangle, donc celui qui va de 1 à 1,5).
Pour le rectangle qui va de 1 à 1,5, on a donc une aire de $g(3 \times 0,5)\times 0,5$.
La somme de tous les rectangles est alors de :
$$\sum_{n=-\infty}^{+\infty} g(n \times 0,5)\times 0,5$$
L’aire en vert n’est pas tout à fait égale à l’aire sous la courbe : parfois il y a des morceaux qui dépassent, parfois il en manque. On peut réduire l’erreur ainsi commise en diminuant la largeur de rectangles.
En fait, diminuons la largeur des rectangles de façon infinie : chaque rectangle a désormais une largeur infiniment petite. Sa largeur est notée $dx$, signifiant « une variation infiniment petite sur x ».
À ce niveau, chaque rectangle infiniment fin a une hauteur égale à $g(x)$ et une largeur égale à $dx$.
La somme de tous les rectangles est donc logiquement :
$$\sum_{n=-\infty}^{+\infty} g(x) dx$$
Or ici, le nombre $n$ n’a plus aucun sens : en effet, vu que $dx$ est infiniment petit, ça n’a plus de sens de les dénombrer.
Dans ce cas là, on utilise non plus la notation de la somme discrète (ou discontinue) $\sum$ mais la notation d’une somme prévue pour calculer les intégrales : la somme intégrale noté avec le symbole « s long » : $\int$.
L’origine de ce symbole correspond à un « S » référant au mot « somme ».
On l’utilise donc ici pour désigner l’aire sous la courbe quand on utilise l’approximation des rectangles de largeur infiniment petites :
$$\int_{-\infty}^{+\infty} g(x) dx$$
Cette intégrale ne peut plus vraiment se mesurer graphiquement. On résout ceci en calculant la primitive de la fonction.
Le théorème fondamental de l’analyse (un théorème de base en math) dit que l’aire sous la courbe d’une fonction est égale à la primitive de cette fonction. Cacluler l’aire ou calculer la primitive revient donc à la même chose.
Pour notre fonction $g$ de départ, on a donc :
$$F(x) = \int g(x) dx$$$$F(x) = \int {(-3x^3+5x^2+5)} dx$$
Et avec les règles de calcul sur les intégrales des polynômes il vient :
$$F(x) = \frac{3}{4}x^4 + \frac{5}{3}x^3 + 5x$$
Il n’y avait pas une histoire de constante d’intégration ?
La primitive $F$ est la fonction qui prends $f$ pour dérivée.
Maintenant prenons ces deux fonctions :
$$I(x)= x^2$$$$J(x)=x^2 + 3$$
La dérivé de chacune d’elle est égale à $k(x) = 2x$.
Dans ce cas, quelle est la primitive de la fonction $k$ : est-ce que c’est $I$ ou $J$ ?
En fait, il s’agit des deux fonctions.
Quand on calcule la primitive d’une fonction, on doit ajouter une constante : ainsi, la primitive de la fonction $cos(x)$ est $sin(x)+\text{Constante}$.
Ajouter une constante à une fonction, ça revient à ajouter le même nombre pour chaque valeur de la fonction. Graphiquement, cela fait monter ou descendre la courbe :

Si la courbe ne fait que monter, alors la variation de la fonction ne change pas : les dérivées sont donc identiques à chaque fois.
Dit autrement, pour chaque fonction, il y a plusieurs primitives qui ne diffèrent entre-elles que par la valeur de d’une constante, d’où le « $+ Constante$ » que l’on doit ajouter.
En pratique, quand on doit calculer la primitive d’une fonction, il est donné une condition initiale : une information supplémentaire qui permet de déterminer précisément cette constante. Par exemple, si on vous dit de calculer la primitive $L(x)$ de la fonction $l(x) = -sin(x)$ et qu’on vous dit que $L(0) = 2$, alors vous pouvez déterminer la primitive de $l(x)$ :
$$L(x) = \int l(x) dx$$$$L(x) = \int -sin(x) dx$$$$L(x) = cos(x) + \text{Cste}$$
On sait que $L(0) = 2$. On a donc $2 = cos(0) + \text{Cste} = 1 + \text{Cste}$. Donc, $\text{Cste} = 1$.
La détermination de la constante d’intégration se fait toujours à l’aide d’une condition qui est soit donnée, soit à déterminer. En physique, il peut s’agir de l’altitude d’un objet au moment du lâcher, ou bien la vitesse à l’instant 0…
Intégrales multiples
Résumons ce qu’on a vu jusqu’à présent :
- On avait une fonction $g$ dont on voulait l’aire sous la courbe car cette aire correspond à l’intégrale de la fonction.
- Notre première approche a été d’utiliser des rectangles pour mesurer l’aire car c’est plus simple avec des rectangles.
- Les rectangles laissant des espaces vides sous la courbes, j’ai dit qu’on pouvait être plus précis en diminuant la largeur de ces rectangles.
- On a poussé ce raisonnement au bout : la largeur des rectangles est maintenant infiniment petite.
- Pour calculer une somme d’un nombre infini d’éléments infiniment petit, on utilise la somme intégrale avec le symbole $\int$.
Bon : ici, c’est la largeur des rectangles qui était infiniment petite, il fallait donc faire une intégration sur la variable $x$. C’est pour ça que l’on a mis $dx$ dans l’expression des intégrales :
$$G(x) = \int g(x) dx$$
Imaginons maintenant que nous ayons non plus une courbe dépendant d’une variable, mais une surface en 3D qui dépend de deux variables :
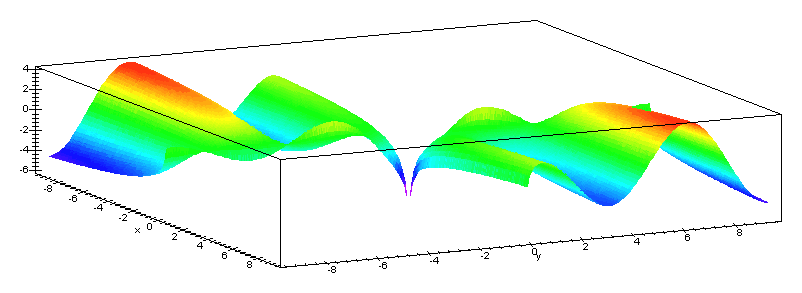
Ici, l’altitude $x$ dépend à la fois de l’ordonnée $y$ et de l’abscisse $x$. Pour calculer, de façon similaire, le volume sous la courbe, il faut utiliser une double intégrale. On applique alors l’intégrale sur $x$, puis dans la foulée sur $y$ :
$$F(x,y) = \int_x\int_y f(x,y) dx dy$$
On peut le voir de cette façon : si vous devez empiler des cartons dans votre garage : vous commencez à créer une ranger de carton en bas. Quand la première rangée est faite, vous faites une rangée juste au dessus. Puis quand tout le mur est recouvert de cartons, vous recommencez avec une nouvelle « couche » de cartons.
Vous intégrez donc votre garage selon des lignes de carton empilées, puis selon des « couches » de cartons.
En math, on intègre la fonction selon une première variable $dx$ puis selon une seconde variable $dy$, jusqu’à avoir déterminée le volume intégral sous la courbe.
En pratique, on peut très bien avoir 2, 3, 4… voir plus d’intégrales successives. En soit, ça ne correspond qu’à une succession d’intégrales simples, à chaque fois sur une variable différente.
Pour prendre un exemple, dans la loi physique des gaz parfaits, $P \times V = nRT$, la température $T$ est dépendante à la fois du volume $V$ et de la pression $P$. Si on fait varier $V$ et $P$, la température va changer. En utilisant une intégrale double, on sait calculer la température lorsque le volume et la pression varient : il suffit de considérer que le volume et la pression varient de façon indépendante, puis d’intégrer successivement par rapport au volume puis à la pression (ou inversement).
Intérêt des intégrales
Tout comme les dérivées ont des applications en physique, les intégrales en ont aussi.
Par exemple, en thermodynamique, on utilise les intégrales pour modéliser le comportement d’un gaz lors de la détente ou de la compression : on étudie ce gaz quand la variation de pression est infiniment petite : les fonctions de température et de volume vont alors évoluer en fonction de la pression : c’est à la base du fonctionnement d’un moteur thermique, d’une pompe à chaleur, d’un climatiseur ou d’un frigo. Sans le calcul d’intégrales, ces appareils n’existeraient pas, ou auraient un rendement bien plus mauvais.
On s’en sert également en dynamique des fluides pour modéliser l’écoulement d’un fluide, ou en électricité pour déterminer le champ magnétique ou électrique qui règne autour d’une particule.
Les intégrales et les dérivées sont fortement liées : l’une est inverse de l’autre, et on les retrouve bien souvent de façon simultanée.