
Par rapport aux pendules à balanciers et les montres mécaniques, les montres à quartz ont nombres d’avantages : non seulement ils fonctionnent partout (une pendule à balancier fonctionne très mal en mer et pas du tout en apesanteur), mais elles sont aussi beaucoup plus précises : elles ne dévient que de quelques secondes tous les mois (contre plusieurs minutes par jour pour les autres). elles n’ont pas non plus besoin d’être remontées tous les soirs : elles fonctionnent des années avec une petite pile bouton.
Toutes ces pendules et ces montres (y compris les horloges atomiques d’ailleurs) ont besoin d’un système oscillant pour pouvoir compter les secondes qui passent. Le balancier d’un pendule oscille par gravité, et une montre mécanique utilise l’oscillation d’une roue dentée sur un ressort spirale.
La montre à quartz, elle, utilise un cristal de quartz, dont l’oscillation est rendue possible par effet piézoélectrique.
J’explique l’effet piézoélectrique en détail dans mon article précédent : D’où vient l’effet piézoélectrique ?. Ici, je vais expliquer comment l’effet piézoélectrique est exploité dans une montre à quartz et comment ce petit morceau minéral permet de donner l’heure.
Le besoin d’un système oscillant pour donner l’heure
Donner l’heure revient à compter les secondes qui passent. Pour cela, il faut déjà savoir ce qu’est une seconde : combien elle dure. Il faut aussi un système qui permette de compter plusieurs secondes de suite.
Dans une pendule à balancier, la seconde est obtenue depuis le balancier. On doit à Galilée l’étude du pendule pesant : c’est lui qui a découvert que toute masse suspendue à un fil se balançait avec un rythme constant dépendant de la longueur du fil et indépendant de la masse suspendue au bout et de l’amplitude du mouvement. Les travaux de Galilée, ainsi que ceux de Huygens peu après, furent à l’origine de la première horloge à balancier : ce dernier utilisait un pendule dont la longueur donnait une oscillation d’une seconde exactement.
À l’époque, la seconde était définie comme un soixantième de la minute, elle-même définie comme le soixantième de l’heure. L’heure était le vingt-quatrième de la rotation terrestre, qui elle est bien-sûr pré-définie.
En fixant la longueur du balancier, il suffit de pousser le pendule et de compter les oscillations : 60 donnaient la minute, 3 600 donnaient l’heure et 86 400 donnaient la journée.
Dans l’horloge, ce comptage est obtenu par des roues dentées, et le balancement, par des ressorts et des masses suspendues. Quand les masses descendaient au cours de la journée, leur énergie potentielle était transmise au pendule et à tout le mécanisme.
Plus tard, naquirent les mécanismes à ressort : le ressort avait une raideur bien précise et oscillait avec un rythme fixe. Ces systèmes étaient plus précis que le balancier et fonctionnaient même sur un navire, là où le balancier ne supportait pas les mouvements du bateau. Ceci constitua une révolution dans le monde de la navigation, qui utilisait surtout des sabliers avant ça.
En effet, pour se repérer en mer, loin de tout, il fallait connaître l’heure. Grâce à l’heure et connaissant la position des astres dans le ciel, on pouvait déterminer sa position. Par exemple, à Greenwich à midi, le Soleil se trouve au plus haut (à son point de culmination). Si, à midi, le Soleil se trouve décalé de +15°, alors on sait qu’on se trouve à 900 milles nautique à l’ouest de Greenwich. Toutes ces données étaient répertoriées dans des tables, mais un instrument de mesure du temps restait nécessaire (la latitude quant-à-elle était obtenue avec un astrolabe ou un sextant).
Pendule pesant ou ressort circulaire, tous utilisent un système oscillant pour donner le rythme, définir la seconde et calculer le temps qui passe.
Les montres électroniques à quartz n’échappent pas à la règle : il faut quelque chose qui puisse donner le rythme à tout le mécanisme. Dans les montres à quartz, c’est le cristal de quartz qui se charge de vibrer avec une fréquence très précise et très stable.
Dans la montre à quartz
Le cristal de quartz d’une montre à quartz se trouve dans un composant bien précis, l’oscillateur :

Ce quartz, taillé en forme de diapason, mesure quelques millimètres de long seulement et se trouve dans un composant scellé.
Comme je l’explique dans l’article sur l’effet piézoélectrique, quand on envoie un courant électrique sur un cristal de quartz, ce dernier se déforme. Quand on coupe le courant, le cristal reprend sa forme initiale. Si on applique une tension alternative, alors le cristal vibre.
Le problème d’un tel système est de choisir la fréquence du signal électrique à appliquer sur le cristal ? En effet, c’est justement ce qu’on cherche avec l’oscillateur !
La solution est d’utiliser la fréquence propre du cristal.
Tous les objets ont une fréquence de vibration propre : une fréquence à laquelle ils vibrent naturellement. Tout le monde a par exemple déjà plaqué une règle en plastique ou en métal sur une table et fait vibrer le bout de la règle pour faire du bruit. Tout le monde a donc aussi constaté que la vibration de la règle et le son émis dépendait de la longueur de la règle. En adaptant la longueur de la règle, on peut choisir la fréquence sonore qu’elle va émettre quand on joue avec.
C’est cela qu’on fait avec le quartz : les cristaux intégrés dans les montres sont taillées très précisément pour que leur fréquence propre soit de 32 768 Hz très exactement (je reviendrai sur cette valeur un peu plus bas). Lorsque l’on envoie une impulsion électrique dessus, le cristal se met à vibrer brièvement à cette fréquence.
Or, un cristal piézoélectrique qui vibre émet lui-même un signal électrique ! Ce signal électrique en provenance du cristal est capté par un circuit électrique.
Notre règle cesse de vibrer après un petit moment. Pour continuer à faire du bruit, il faut l’actionner de nouveau, encore et encore. Pour le quartz c’est pareil : la vibration s’atténue vite. Il faut donc envoyer une nouvelle impulsion électrique. L’astuce ici est de renvoyer dans le quartz le signal qu’il a lui-même émis (après l’avoir amplifiée). Comme ça, le quartz est maintenu en vibration par sa propre fréquence (qui est aussi sa fréquence propre). L’ensemble est un système auto-asservi et est assuré de fonctionner sur la fréquence propre du quartz.
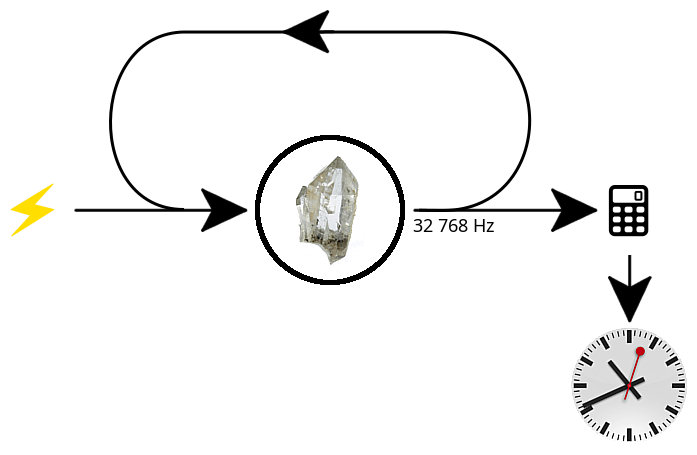
Il reste alors à capter la fréquence du signal électrique émis par le quartz, de compter les oscillations, et de dire qu’une seconde passe quand on a compté 32 768 oscillations :
Pourquoi 32 768 Hz ?
On peut tailler un cristal (et n’importe quel objet) de façon à ce qu’il oscille à n’importe quelle fréquence. Alors pourquoi ne pas avoir taillé un quartz pour qu’il oscille à 1 seconde ? Pourquoi 32 768 Hz ?
Déjà, généralement, plus un objet est grand, plus sa fréquence propre est faible. On le voit bien avec une pendule à balancier : l’oscillation de 1 seconde est obtenue avec un balancier de 1 mètre environ. Pour une montre, il faut forcément un système plus petit et donc vibrant plus vite.
Ensuite, un système qui vibrerait fait également vibrer l’air autour de lui à cette fréquence. Ceci est pratique pour les diapasons et les instruments de musique, mais pas pour les montres. Il faut donc une fréquence qui soit supérieure à environ 20 000 Hz (limite d’audibilité humaine) pour que la montre n’émette pas un bruit strident en continu.
Enfin, dernier paramètre : la technologie utilisée. Le mécanisme de la montre est électronique. Par conséquent, il fonctionne en base 2, avec du binaire. Or, bienqu’il soit possible de faire des calculs en base 10 avec un appareil numérique, cela pose problème dans certains cas. Certains nombres décimaux sont non représentables en base 2. Si l’on ne fonctionne pas en base 2, on se retrouve automatiquement avec des valeurs approchées à certains endroits.
Si on résume, il faut donc une fréquence :
- suffisamment élevée pour que l’oscillateur puisse être mis dans une montre ;
- supérieure à 20 kHz ;
- puissance de 2.
Or, la première puissance de 2 qui satisfait à la seconde condition est $2^{15}$. Elle satisfait aussi à la première. Et $2^{15}$, vous le devinez, ça correspond à 32 768 !
Les cristaux de quartz sont donc taillées très précisément de façon à ce que leur fréquence propre soit exactement de 32 768 Hz. Ensuite, un simple compteur binaire sur 15 bit permet, par 15 divisions successives par 2, de transformer la fréquence d’oscillation du quartz en un signal dont la fréquence est de 1 Hz.
C’est ce dernier signal qui est envoyé au moteur du mécanisme et qui actionne la trotteuse. Un système d’engrenages relié à la trotteuse permet ensuite de faire tourner les aiguilles des minutes et des heures (respectivement 60 fois et 3 600 fois plus lentement) et parfois les aiguilles des jours ou des mois selon les montres.
Sur une horloge à affichage numérique/digital, le signal numérique de 1 Hz active l’affichage des chiffres, sans passer par un système mécanique et des aiguilles.
Conclusion
La montre à quartz utilise un cristal vibrant à $2^{15}$ hertz. Cette fréquence est inaudible et adaptée à la fois à la taille et au système numérique de la montre. Les vibrations sont obtenues en envoyant une impulsion de départ sur le cristal, puis en captant le signal piézoélectrique du quartz et en la renvoyant sur le cristal : ce dernier vibre donc continuellement à sa fréquence propre. Enfin, un petit moteur relié à un compteur électronique fait bouger la trotteuse chaque fois que le compteur compte 32 768 oscillations.
Ce système de cristal en vibration est utilisé partout. C’est un cristal qui produit le signal de 2,4 GHz du Wi-Fi ou du Bluetooth. Plus généralement, ce sont des cristaux qui permettent d’obtenir les fréquences d’émission et de réception dans n’importe quel système de télécommunication.
Même les ordinateurs intègrent plusieurs cristaux vibrant un peu partout : il faut bien compter la fréquence du processeur, la fréquence de la puce Wi-Fi, le débit de l’USB et même tout simplement compter les secondes qui passent : il y a une montre à quartz dans tous les ordinateurs et c’est elle qui donne à l’heure à votre ordinateur même lorsque vous n’êtes pas connectés à Internet ou que l’ordinateur est en veille ou éteint.
Enfin, pour finir, je ne peux qu’insister sur l’importance d’avoir un système périodique pour compter le temps qui passe. Sans ça, nous ne pourrions pas mesurer l’écoulement du temps.
Quand on y pense, c’est la rotation journalière de la Terre qui permet de compter les jours. Ce sont les rotations périodiques de la Terre autour du Soleil qui permettent de compter les années. On ne peut pas compte le temps qui passe sans avoir une référence de durée quelque part.
Dans tous les systèmes de mesure du temps, de la clepsydre à la montre à quartz, en passant par le sablier ou le pendule, ce sont les systèmes périodiques qui donnent le rythme au système et permettent de compter le temps qui passe (pour le sablier et la clepsydre, la période est un débit : quantité de sable ou d’eau par unité de temps).
Même les horloges atomiques fonctionnent ainsi : la fréquence de base est donnée par la fréquence des radiations émises par une transition énergétique bien précise d’un électron d’un atome de césium 133.
Le balancier d’un pendule se balance à un rythme fixe seulement sur Terre (le rythme changerait sur les autres astres, à cause de l’accélération de la pesanteur qui est différente). Une montre à quartz est précise, car le morceau de quartz est taillé précisément. En utilisant un atome de césium 133, on a une précision incroyable directement fournie par la nature, et valable partout, tout le temps et qui soit inusable : c’est ce qui se passe dans une horloge atomique.