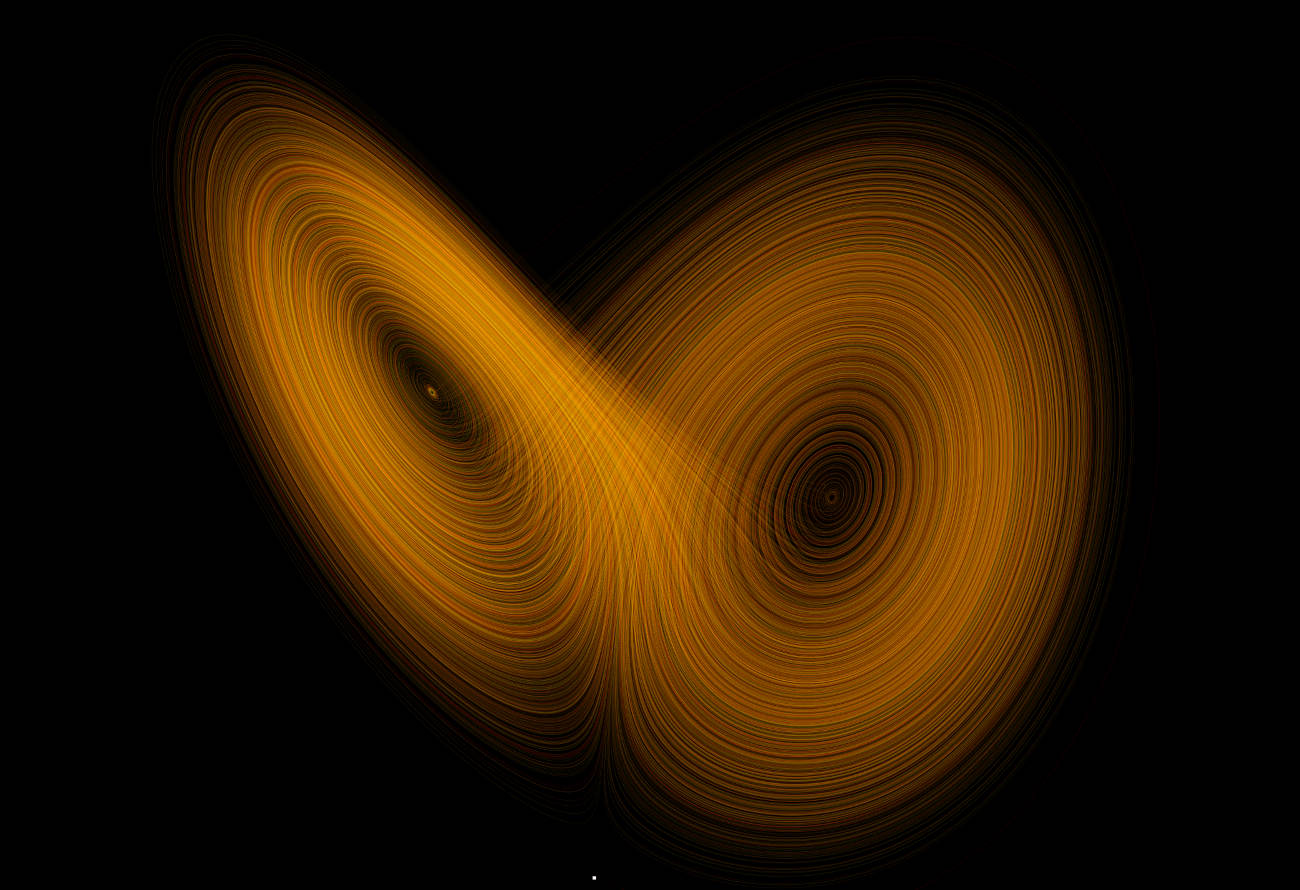
À l’image de ce que j’avais fait pour les figures de Mandelbrot, où j’avais expliqué ce qu’on voyait lorsqu’on avait une figure de Mandelbrot (les fractales) sous les yeux, voici le moment de faire la même chose pour les figures « en papillon » d’un attracteur de Lorenz.

Je suis à peu près sûr que tout le monde les a déjà vu et que tout le monde les associe au chaos, à l’effet papillon, etc. Je pense également que très peu de gens ne savent ce que ces figures représentent vraiment.

Et c’est bien dommage.

En effet, ces figures en papillon sont plutôt jolies et complexes. Les fonctions mathématiques qu’elles représentent sont pourtant simples (c’est du niveau lycée), mais elles sont utilisées d’une façon qui permet de faire ressortir des comportements assez particuliers dans les nombres.

Un système chaotique

Dans le langage courant, quand on parle d’une situation chaotique, on parle de quelque chose de désordonné, confus, ou encore imprédictible.

Pourtant, en réalité, un système chaotique est tout sauf imprédictible. Bien au contraire : tous les systèmes correctement décrits par des équations sont parfaitement déterministes.

Dans ces conditions, un système est chaotique s’il est particulièrement sensible aux conditions initiales. Cela veut dire que vous n’avez qu’à changer très légèrement un seul paramètre initial, et le système évoluera de façon totalement différente !

Comme système non chaotique, on peut prendre la chute des corps : que l’on fasse tomber une pomme de 1,0 mètres ou de 1,0001 mètres, la pomme tombera par terre et au même endroit : le résultat sera identique.

Comme système chaotique, prenons un ensemble de boules de billard que l’on vient frapper. Même en étant très précis, vous ne pourrez jamais taper exactement au même endroit et avec la même force deux fois de suite. Résultat, vous n’aurez jamais deux parties qui vont se ressembler :

Comme il n’a suffi que d’un tout petit écart au moment de la frappe pour obtenir un résultat totalement différent, on dit que le jeu du billard est un système chaotique.

Cela ne veut pas dire que l’issue du jeu ne soit pas prédictible pour tant. Car dès l’instant où l’on a frappé la boule blanche, on connaît sa vitesse et sa position, et donc là où elle va aller et avec quelle force. On peut donc déterminer où chaque boule va se rendre, si l’on connaît leur position également. En tout cas, en théorie on peut déterminer tout ça.

Le côté chaotique découle simplement du fait que taper un tout petit peu à droite, ou un tout petit peu à gauche va modifier complètement le comportement des boules.

Ceci rejoint le fameux « effet papillon », selon lequel le vent produit par le battement des ailes d’un papillon va totalement modifier les écoulements de l’air et finir par produire un ouragan 10 000 km plus loin.

Et les figures en papillon ?

Les figures des attracteurs de Lorenz, appelées « figures en papillon » apparaissent en 1963 grâce au météorologue Edward Lorenz.

Lorenz cherchait à modéliser l’atmosphère et à comprendre son comportement. Pour faciliter les calculs, il mit au point un triplet d’équations, censé représenter de façon très simplifiée un système particulièrement sensible aux paramètres initiaux :

$$\begin{cases} \frac{dx}{dt} = \sigma \left(y(t) - x(t) \right) \\ \frac{dy}{dt} = \rho \text{ }x(t) - y(t) - x(t)z(t) \\ \frac{dz}{dt} =x(t)y(t) - \beta \text{ }z(t) \end{cases}$$

Où $\sigma$, $\rho$ et $\beta$ (lire sigma, rho et beta) sont des paramètres numériques, de simples nombres (positifs ici), qui font varier les fonctions.

x, y, et z sont les fonctions décrivant les positions sur les trois coordonnées à un moment t donné. dx/dt, dy/dt, dz/dt sont les fonctions dérivées, décrivant la variation de ces trois coordonnées au cours du temps.
Enfin, on constate que chaque coordonnée dépend des deux autres.

L’ensemble produit le tracé d’une courbe dans un espace en trois dimensions, comme celle sur la figure d’en-tête. Cette figure est réalisée en itérant 2 millions de fois le programme pour obtenir l’évolution à relativement long terme (d’où le grand nombre de boucles visibles).

Systèmes stables et instables

Généralement, un système quelconque tend soit vers une situation stable, soit vers une situation instable.

Dans le cas d’un système stable, cela se traduit par un « point fixe » sur la figure de Lorenz : un point de l’espace où la courbe semble se diriger quoi qu’il arrive :

Dans cet exemple, on part du point blanc et on laisse faire les fonctions. On remarque que si on itère assez longtemps, la courbe converge vers le point central de « l’aile » droite du dessin du papillon. Peu importe ce qu’on fait : si la fonction est stable, la fonction convergera vers ce point point, même si l’on partait d’un autre point blanc.

Tous les systèmes ne sont pas comme ça. Certains — beaucoup même — sont instables.

Dans ce cas, la figure en papillon présente des « ailes » entre lesquelles la courbe semble osciller. Les oscillations peuvent ne jamais se stabiliser complètement. C’est le cas pour la figure suivante :

Ici, le système est instable : on peut itérer autant que l’on veut, la figure oscillera de façon instable entre la gauche et la droite, sans jamais se décider à converger vers un point fixe.

Remarquez que ces deux figures sont faites avec des paramètres très proches. La seule différence est le β, dont le onzième chiffre après la virgule passe de 6 à 7 (donc un changement de 0,000000001 % sur un seul des trois paramètres). C’est tout ce qu’il aura fallu pour passer d’un système stable à instable.

Le point de départ d’où part la courbe, peut lui aussi être paramétré. Pour chaque point de départ existe donc une courbe de Lorentz. On peut dès lors créer une animation où l’on voit les positions instantanées de plusieurs points simultanément (et non pas comme j’ai fait, un seul point évoluant avec le temps).

On constate alors qu’avec le système d’équation de Lorenz, tous les points finissent par tourbillonner autour d’une figure de Lorenz. On dit que cette figure « attire » tous les points autour de lui, d’où son nom « d’attracteur ».
On peut en voir une animation sur Wikipédia : les 25 000 points finissent sur des orbites autour de l’attracteur, comme des astres autour d’un trou noir.

Cela modélise le fait que tous les points d’un ensemble finissent par osciller de façon chaotique. Autrement dit, pour un système physique décrit avec des équations comme ça, il n’existe pas de comportement stable : ce système est instable ou chaotique. C’est par exemple le cas d’un double pendule (un pendule accroché au bout d’un autre pendule), ou encore de l’évolution des masses d’air en météo, ou celle d’un ensemble de parties de billard.

Conclusion

À la question « que voit-on sur une figure de Lorenz ? », on peut donc répondre qu’il s’agit de la courbe représentative d’un système d’équations bien choisies. Rien de plus difficile. La chose intéressante est alors la nature même de cette courbe : ce n’est pas n’importe laquelle. Cette courbe est celle d’un système chaotique.

Ces fonctions modélisent des systèmes parfaitement déterministes, mais non-déterminables en pratique. Dans l’exemple plus haut, on voit qu’une variation d’un milliardième de pourcent sur un seul des paramètres suffit pour passer d’un système stable à un système instable.

C’est ça la définition d’un système chaotique : tout est prédictible, à condition d’avoir une mesure très précise des données de départ. On peut la résumer avec cette belle phrase :

Les systèmes chaotiques sont par définition déterministes mais non déterminable.

Ceci est exactement ce qu’on fait en météorologie (qui est d’ailleurs ce sur quoi Edward Lorenz travaillait).

Prévoir le temps est difficile, car il y a des centaines de paramètres à prendre en compte, et l’évolution des courants d’air et des particules de l’atmosphère ont des comportements chaotiques. On arrive donc à prévoir à peu près la température sur un jour ou deux, peut-être trois, mais au-delà, ce sont seulement des « suppositions éclairées », avec des faibles indices de confiance.

Dans tous les cas, et c’est pourquoi j’ai écrit cet article au départ : les figures des attracteurs de Lorenz, ou « figures en papillon » sont jolies et suscitent la curiosité. Elles ne sont pas difficiles à créer. Quelques lignes de code suffisent. Les images de cet article proviennent de mon générateur de figures de Lorenz que j’ai fait pour l’occasion (n’hésitez pas à changer la couleur, l’épaisseur du trait, le nombre de points…) : Générer des figures de Lorenz.