
En maths, peut-être avez-vous déjà rencontrés les fonctions hyperboliques : cosinus hyperbolique (cosh), sinus hyperboliques (sinh).
Et peut-être comme moi, vous est-il venu à l’esprit qu’il faut être tordu pour appeler une fonction ainsi. Et bien en fait le nom de ces fonctions n’est pas choisit au hasard (mais les profs n’en parlent pas en cours).
Cet article ne vous donnera pas toutes les propriétés des fonctions hyperboliques, mais vous permettra de comprendre d’où elles viennent.
Les fonctions circulaires
Avant de parler de sinus hyperboliques et de cosinus hyperbolique, parlons de sinus et cosinus. Ces deux fonctions sont connues depuis le collège. Elles tirent leur origines des cercles et des triangles comme on va le montrer : commençons par tracer un cercle. Puis, en plaçant un point quelconque sur le cercle, on peut constituer un triangle formé par ce point et par le diamètre du cercle :
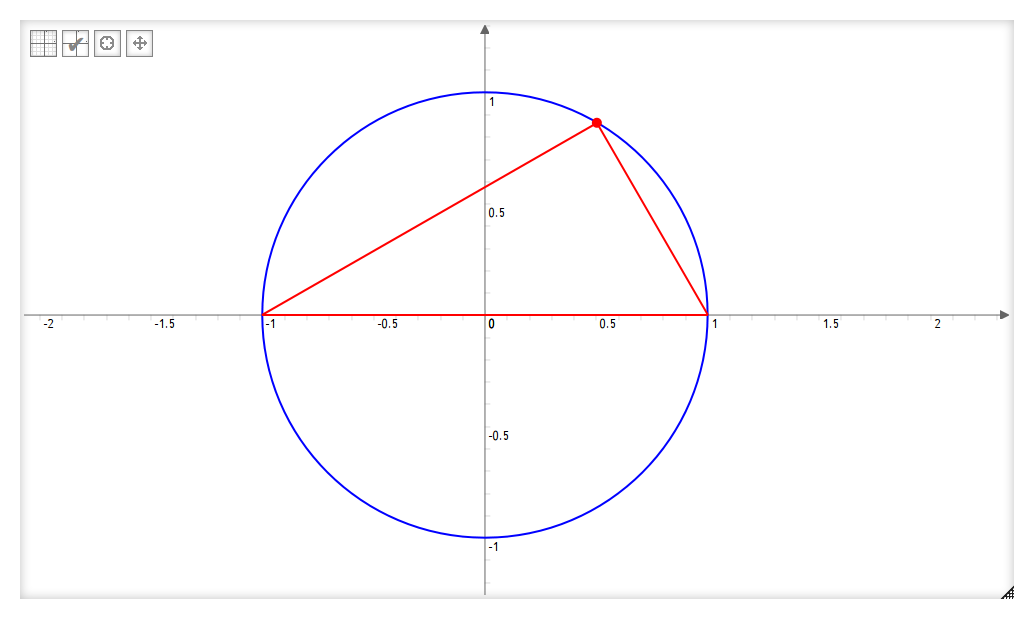
Le cercle étant alors circonscrit au triangle voit son diamètre être également un des côtés du triangle : ce triangle est rectangle (ceci est valable quelque soit la position du point sur le cercle !).
On peut alors utiliser les fonctions sinus et cosinus, qu’on retrouve dans le cercle :
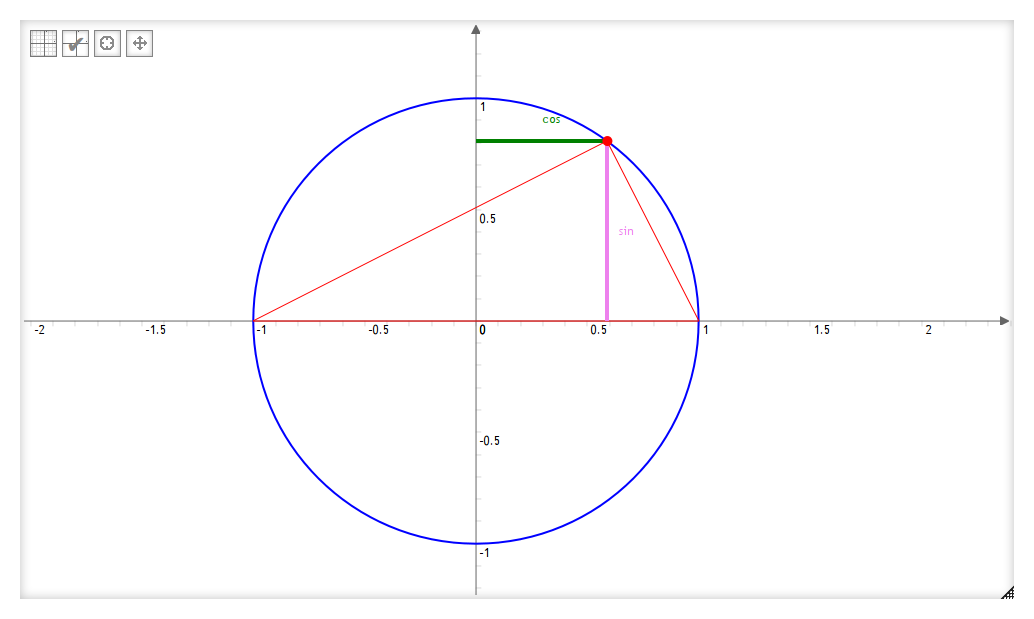
Le point peut-être placé n’importe où, l’angle qu’il forme avec l’origine permettra toujours de calculer un sinus et un cosinus.
Pourquoi tout ça ? Vous allez comprendre.
Pour trouver le sinus et le cosinus, on a pris un cercle et un point sur ce cercle. Les fonctions sinus et cosinus dans ce cas là sont appelés sinus circulaire et cosinus circulaire, en référence à la figure du cercle que l’on a pris.
Les fonctions hyperboliques
Je pense que vous voyez où je veux en venir : dans le cas des fonctions hyperboliques, ce n’est donc pas un cercle qu’on a pris, mais une hyperbole (d’équation $x^2-y^2=1$) :

Les fonctions hyperboliques (co)sinus hyperbolique, (co)tangante hyperbolique, leur inverses et bien d’autres sont issues de cette géométrie là, où on a remplacé le cercle par une hyperbole.
Ces fonctions sont similaires à leurs homologues circulaires, avec des propriétés qui leur sont propres.
Vous pouvez observer les fonctions cosinus-hyperbolique et sinus-hyperbolique dans l’image d’en-tête. Vous pourrez constater qu’elles n’ont rien à voir avec les fonctions trigonométriques circulaires.
Pour les tracer, rendez-vous sur cet outil : Tracer des graphiques, utilisez les fonctions $cosh(x)$, $sinh(x)$ ou $tanh(x)$ (constatez par exemple que $sinh(x)+cosh(x)$ est égal à $exp(x)$).
À la place du cercle ou de l’hyperbole, on pourrait aussi prendre n’importe quelle figure : en plaçant un point sur cette dernière il sera tout à fait possible de trouver une fonction qui donne les coordonnées de ce point, en fonction de l’angle avec l’origine. Ça n’a juste pas tellement d’intérêt : le cercle et l’hyperbole (toutes les deux la famille des coniques) sont des figures particulières avec de nombreuses propriétés mathématiques.
Tout comme pour les fonctions trigonométriques circulaires, il y a des tas d’applications pratiques. Par exemple en astronomie et en astronautique : quand un astéroïde frôle la planète Terre, si sa vitesse est suffisante, sa trajectoire décrit une hyperbole. Les forces gravitationnelles entre la Terre et l’astéroïde peuvent nécessiter des fonctions hyperboliques. Même chose pour le lancement d’un satellite ou d’une sonde spatiale : leur trajectoire est parfaitement calculée et ce calcul a nécessité des fonctions hyperboliques.
Liens
- Les fonctions trigonométriques : article détaillant les fonctions trigonométriques qui existent en plus de sinus et cosinus, qui ne sont que deux fonctions parmi plein d’autres !
Et mes deux autres articles de vulgarisation mathématique :