
C’est sûrement le théorème de géométrie le plus connu (on l’apprend au collège), mais savez-vous le démontrer ?
Le nombre de ses démonstrations (mathématiques et/ou géométriques) ne manquent pas, mais celle que je vais vous présenter ici me semble la plus simple à apprendre : c’est la démonstration par la soustraction des aires, que l’on doit à Abraham Garfield (1831-1881), vingtième Président des États-Unis.
Elle est en effet très courte et on a seulement besoin des identités remarquables et de la formule de l’air d’un triangle rectangle :
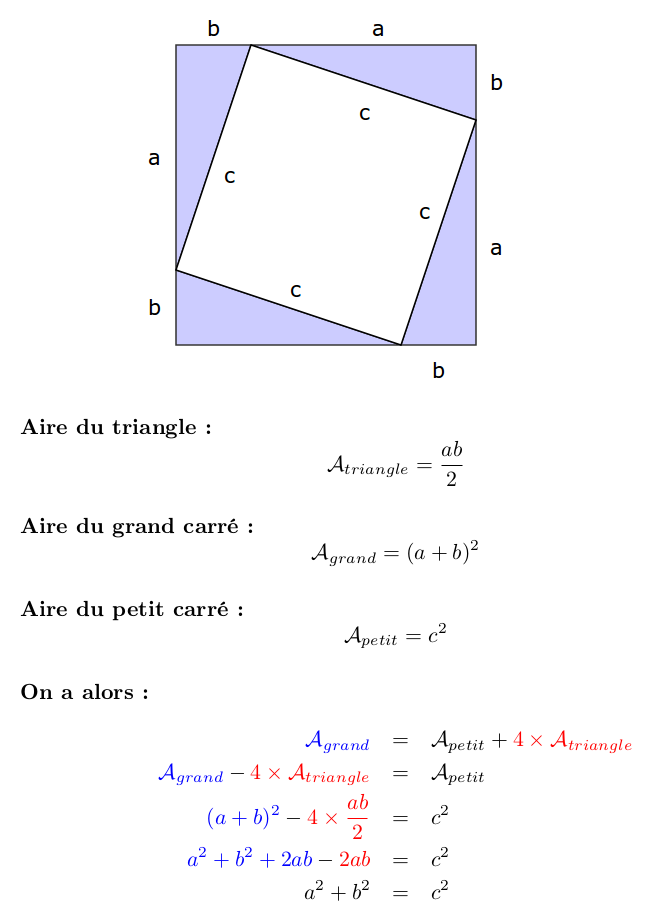
Dans le principe, on remarque simplement que le grand carré extérieur est formé de quatre triangles rectangles identiques et du carré centrale. Ensuite, on simplifie et on fait en sorte de trouver la formule de Pythagore.
Édit : comme Arzhurb me fait remarquer dans les commentaires, il faut montrer que le quadrilatère central (en blanc) est un carré.
Le quadrilatère est un losange : ses côtés sont tous d’égales longueur, par construction.
Il reste à montrer qu’il est un carré : pour ça il suffit de montrer qu’un des angles est droit.
En prenant un des côtés du grand carré extérieur (carré par construction) comme un angle plat de 180°, on peut le décomposer en trois angles : le petit angle d’un triangle, le grand angle d’un triangle et enfin l’angle du quadrilatère. Or, on sait que la somme des angles d’un triangle est de 180°. En retirant l’angle droit — les triangles étant rectangles — il reste 90°. Ceci correspond à la somme des deux autres angles — le petit et le grand restant. L’angle du quadrilatère de côté C vaut donc 180° – 90° = 90°.
Le losange est alors droit : il s’agit bien d’un carré.