
Un peu dans la suite de l’article que les équations de Maxwell, je vais tenter d’expliquer à quoi correspondent les dérivés utilisés en math et apprises au lycée.
Les fonctions
Déjà, commençons par expliquer ce qu’est une fonction.
Une fonction $f(x)$ sert à appliquer une opération $f$ sur un nombre $x$ et on obtient un autre nombre $f(x)$ en résultat.
C’est utile quand vous voulez appliquer la même opération sur toute une série de nombres. Admettons en effet que nous ayons une liste de nombres {1, 2, 3, …, 99, 100} et qu’on veut prendre le triple et ajouter 2 à chacun d’eux.
Au lieu d’écrire le calcul à chaque fois, on va créer une fonction qui à n’importe quel nombre « $x$ » va appliquer le triple et va ajouter 2 : $$f(x) = 3\times{x}+2$$
Ainsi, pour le nombre 42, on aura : $f(42) = 3\times{42}+2$ ce qui est égal à $128$.
Les fonctions sont très pratiques sur un ordinateur ou une calculatrice programmable : il suffit d’y entrer la fonction et de lui dire de calculer $f(42)$ et il sortira directement le résultat. C’est encore plus pratique si notre fonction est compliquée ou longue à taper à chaque fois et qu’on a beaucoup de nombres à calculer.
Le monde est rempli de fonctions. Prendre une nombre pour le faire passer à travers la moulinette d'une fonction et recevoir un autre nombre en résultat, c'est très courant.
La balance du supermarché qui pèse les légumes et donne le prix ? Une fonction.
La caisse qui sort la TVA sur vos achats ? Une fonction.
Le programme qui calcule une distance dans votre application GPS, applique les vitesses des routes et donne une heure d'arrivée ? Une autre fonction.
Le système qui transforme un signal binaire en couleurs sur votre télé ou en son dans votre MP3 ? Une autre fonction !
Le truc que les matheux font aussi, c'est faire des opérations sur les fonctions, en plus d'en faire sur les nombres simples. L'opération de dérivation est une de ces opérations, et on va voir ce qu'elle implique et à quoi elle sert.
Représenter une fonction
Bon, on a une fonction.
On peut avoir envie d’avoir une représentation graphique : une courbe, pour avoir une visualisation de la fonction.
Par exemple, pour la fonction $g(x) = -3{x^3} + 5x^2 + 5$
En traçant la valeur de $g(x)$ pour chaque valeur de $x$ entre −1 et 2 on obtient cette courbe :

En regardant la courbe, on peut remarquer comment elle varie.
Si on décrit ça, on peut voir ceci (en partant de la gauche et en allant vers la droite) :
- la courbe descend beaucoup au début
- la courbe descend plus lentement
- puis elle remonte un peu
- puis ça redescend un peu
- enfin, la courbe plonge vers le bas.
On peut essayer de traduire cela numériquement, en prenant les règles suivantes :
- si la courbe descend, on met un nombre négatif ;
- si la courbe est stationnaire, on met zéro ;
- si la courbe monte on met un nombre positif.
On obtient quelque chose comme ça :
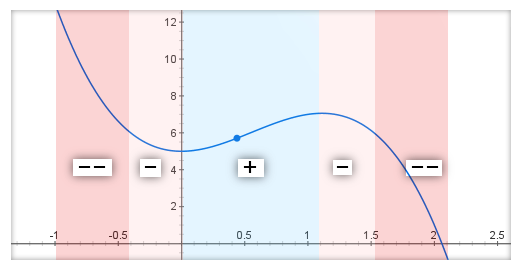
On peut mettre des valeurs numériques sur ça :
- la courbe descend beaucoup au début : on met −3
- la descente diminue un peu : on met −1
- puis elle remonte un peu : on met +1
- puis ça redescend un peu : on met −1
- enfin, la courbe plonge vers le bas : on met −3.
On peut se demander alors : existe-t-il une autre fonction qui possède les valeurs qu’on a mis ici ? Une fonction qui soit à −3, puis −1, puis +1, puis −1, puis −3 ?
Cette fonction existe. On peut la représenter :
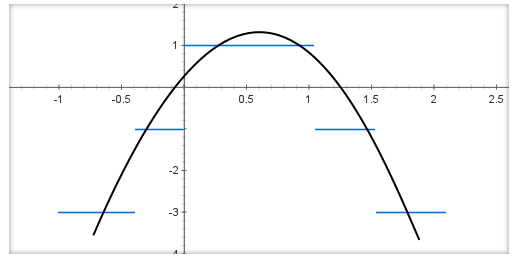
En bleu, on retrouve nos valeurs −3, −1, +1, −1 et −3.
En noir, c’est une courbe qui passe à peu près vers ces valeurs.
Et bien cette courbe représente la dérivée de $g(x)$.
La fonction dérivée
La fonction dérivée de $g(x)$ est notée $g'(x)$ représente les variations de la fonction $g(x)$.
Ici, évidemment, j’ai pris des valeurs approximatives. Si on trace la vraie fonction dérivée de g(x), on obtient très exactement ceci, où $g(x)$ est en rouge et $g'(x)$ est en bleue :

Ma courbe noire précédente n’était pas bien éloignée, hein ?
Pour avoir la valeur de la fonction dérivée en un point donné, il faut connaitre la variation (l’inclinaison) de la fonction principale en ce point. En cours, on apprend qu’il faut tracer la tangente à la courbe et en calculer la pente : en effet, la pente d’une droite est plus simple à mesurer graphiquement que la pente d’une courbe.
La formule pour la courbe bleue $g'(x)$, dérivée de la courbe rouge $g(x)$ est la fonction dérivée : $g'(x) = -9{x^2} + 10x$.
Calculer et tracer la fonction dérivée d’une fonction permet de visualiser la variation de cette fonction. En effet, partout où la fonction dérivée est positive (donc au dessus de l’axe de des abscisses) c’est là où la fonction principale est croissante. Et partout où la fonction dérivée est négative, c’est là où la fonction principale est décroissante. Aussi, voyez que la fonction dérivée a ses racines (endroits où elle coupe l’axe des abscisses) au mêmes endroits où la fonction principale passe de croissante à décroissante ou inversement.
À quoi ça sert ?
Les fonctions dérivées, je me répète, montrent la variation d’une fonction principale. En analysant la dérivée, on obtient donc des informations supplémentaires sur la la fonction principale.
Les applications sont très nombreuses : il arrive que ce n’est pas une valeur qui importe mais la variation d’une valeur. Par exemple en physique, si on prends un champ magnétique, ce dernier n’induit un courant électrique que si il varie (loi de Maxwell-Faraday). Ici, la connaissance du champ magnétique ne suffit pas et il faut connaître sa variation (donc sa dérivée) pour connaître l’intensité du courant induit.
Un autre exemple : la vitesse. Quand on change sa vitesse de déplacement, on subit une accélération ou une décélération : l’accélération existe donc quand la vitesse varie uniquement. L’accélération est donc la dérivée de la vitesse.
Les dérivées existent un peu partout autour de nous. Même si on ne s’en sert pas dans la vie de tous les jours, la science en a beaucoup besoin. Que ce soit en thermodynamique, en chimie ou en électricité, il existe des tas de formules qui font intervenir des dérivées de fonctions.
Notons enfin une dernière chose : en math on utilise la notation « $f'(x)$ » pour désigner la dérivée de la fonction $f(x)$.
En physique et partout ailleurs qu’en math, on notera plutôt $\frac{d(f)}{dx}$, pour signifier qu’on dérive la fonction $f$ par rapport à la variable $x$. Si j’avais mis $\frac{d(f)}{dz}$, ça aurait voulu dire qu’on dérive la fonction $f$ par rapport à la variable $z$.
En physique, il arrive que certaines fonctions ont plusieurs variables (pas juste $x$) et il faut donc savoir par rapport à quoi on la dérive (quelle paramètre varie, en fait) : la température $\frac{d(f)}{dT}$ ? la pression $\frac{d(f)}{dP}$ ?
Bref, les dérivées ce n’est pas juste un délire de mathématiciens.
Je sais très bien qu’en cours on vous pond ça comme un cheveu sur la soupe en vous disant « apprends », mais il y a vraiment un concept derrière : une fonction dérivée traduit la façon dont une autre fonction varie, comment elle évolue (monte, descend, stagne), et il y a des tas de disciplines où un paramètre seul n’est pas intéressant mais où la variation de ce paramètre est importante.
Pour aller plus loin, si vous avez envie (de toute façon c’est dans le programme de Math :p), vous pouvez voir mon article sur les intégrales : les intégrales en math.
L’intégrale d’une fonction, c’est le contraire de la dérivée : si la fonction dérivée $f'$ décrit des variations de $f$, alors l’intégrale $F$ est la fonction dont $f$ décrit les variations.