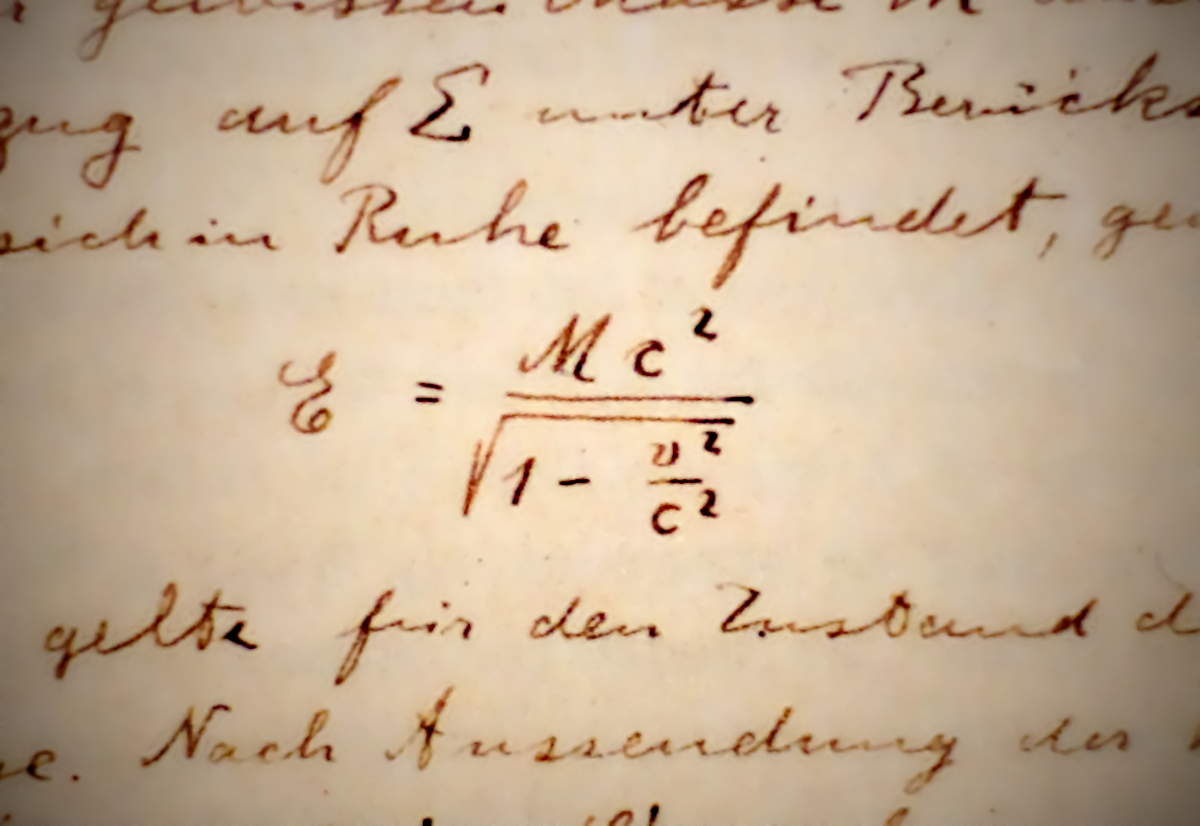
La relativité restreinte (comme la relativité générale) est typiquement associée à Einstein. En effet, et même s’il n’a pas tout inventé, c’est lui qui a assemblé les diverses pièces d’un puzzle en une théorie complète.
Le « principe de relativité » est pourtant bien plus ancien, car il remonte à 1632. À cette époque, Galilée a émis l’hypothèse selon laquelle les lois physiques s’appliquent de façon identique, quel que soit le référentiel dans lequel on se trouve. C’est ça, la relativité.
En l’occurrence, il décrit comment des gouttes d’eau tombent de la même manière que l’on soit dans un bateau à quai immobile ou un bateau se déplaçant en mer.
Sa remarque était pertinente : que l’on soit dans un référentiel immobile ou en déplacement, la chute des corps est identique. Dit d’une autre façon : si l’on se trouve dans une cabine isolée, il est impossible de savoir si le bateau est en mouvement simplement en observant la chute des gouttes d’eau.
D’une façon plus large : toutes les lois physiques s’appliquent de la même façon et avec les mêmes résultats, quel que soit le référentiel, en déplacement [uniforme] ou non.
Ceci constitue le principe de la relativité galiléenne et était accepté assez largement, car logique et sans aucun contre-exemple à l’époque.
Il a fallu attendre la fin du XIXᵉ siècle pour voir apparaître les premiers contre-exemples à ce grand principe ; à savoir les corps qui voyagent à des vitesses proches de celles de la lumière. Pour eux, les lois de la physique classique ne respectent plus le principe de relativité galiléenne.
C’est à partir de ça qu’Einstein publie en 1905 ce qui allait être la relativité restreinte : une théorie englobant la relativité de Galilée et les phénomènes se passant à des vitesses proches de ceux de la vitesse de la lumière. Dix ans plus tard, le même Einstein publiera la relativité générale, englobant la relativité de Galilée, la relativité restreinte et les phénomènes de gravitation.
Même si la vie courante n’en est pas du tout chamboulée, les implications de la relativité d’Einstein sont nombreuses. Dans cet article, je me limite à la relativité restreinte, mais je vais essayer d’expliquer de façon compréhensible quelques-unes de ses (étonnantes) implications.
Principe de relativité
L’une des grandes nouveautés apportées par Einstein avec la relativité restreinte a été de dire que l’écoulement du temps n’était plus uniforme, de même que la notion de distance. Les deux dépendant désormais de la vitesse de déplacement du référentiel que l’on considère.
Pour simplifier, si l’on se déplace, le temps ne s’écoule plus de la même manière et les distances que l’on mesure ne sont plus les mêmes que par rapport à quelqu’un qui ne se déplace pas. Ceci semble absurde, et pourtant… C’est ce que l’on observe !
Prenons un exemple.
Imaginons un bateau voguant à 10 km/h. Maintenant, observons un passager qui marche sur le pont du bateau à 2 km/h dans le sens de navigation. Quelle est sa vitesse par rapport au quai ? 12 km/h ?
En relativité galiléenne — ou mécanique classique — la réponse est bien 12 km/h : car pour obtenir la vitesse du passager par rapport au quai, on effectue l’opération de l’addition entre la vitesse du passager par rapport au bateau et la vitesse du bateau par rapport au quai.
Sauf que… dès la fin du XIXᵉ siècle, on s’est rendu compte, en observant de très hautes vitesses, que les vitesses ne s’additionnaient pas. L’opération pour passer d’un référentiel à un autre n’est pas l’addition !
En analysant les données, Hendrik Lorentz mit au point une opération — la transformation de Lorentz — qui fonctionne pour ces vitesses élevées (ainsi que les plus faibles).
Du coup, la réponse pour la vitesse de notre passager qui marche sur le bateau n’est pas 12 km/h, mais 11,99999987 km/h.
On est numériquement très proche d’une addition : les vitesses considérées sont très éloignées de la vitesse de la lumière, donc les déformations relativistes sont vraiment très faibles.
On peut donc dire que la limite aux faibles vitesses de la transformation de Lorentz est l’addition, et que la limite aux faibles vitesses de la relativité restreinte, c’est la mécanique classique. De même, la relativité restreinte est elle-même une limite aux faibles champs de pesanteur d’une théorie plus vaste appelée la relativité générale :

En somme, si on peut dire, pour nos vitesses, on passe d’une addition :
$$v_{total} = v_{bateau} + v_{passager}$$
À la transformation de Lorentz :
$$v_{total} = \frac{v_{bateau} + v_{passager}}{1+\frac{v_{bateau} . v_{passager}}{c^2}}$$
Où c est la vitesse de la lumière.
On constate que si les vitesses sont petites devant la vitesse de la lumière, alors le deuxième terme du dénominateur tend vers 0. Le dénominateur tend alors vers 1, et l’ensemble tend vers ce qui se trouve au numérateur, donc une simple addition.
Les effets de ce changement d’opération ne sont donc réellement perceptibles que pour les déplacements se faisant à une fraction décente de la vitesse de la lumière.
Implication sur les grandes vitesses
Sur les faibles vitesses, la transformation de Lorentz s’apparente à une addition et donc à la mécanique classique habituelle, mais quid des grandes vitesses ?
Essayons ! Regardons ce qui se passerait si la vitesse du navire et celle du passager étaient proches de la vitesse de la lumière.
On aurait alors :
$$v_{total} = \frac{v + c}{1+\frac{v^2}{c^2}}$$
Au numérateur, on a quelque chose de proche de 2$c$ (vu que v ≈ c).
Au dénominateur, on aura 1 + (~1) ≈ 2.
Au total, on a donc $\frac{2c}{2}$ soit $c$. Dit autrement : à la vitesse proche de celle de la lumière, la lumière se déplace toujours à la vitesse de la lumière !
Étrange, non ?
Pourtant, c’est exactement l’innovation apportée par la relativité restreinte. Les vitesses ne se composent plus par une addition, mais par la transformation de Lorentz. Aussi, ce sont l’espace et le temps qui se « déforment » et au final, cette équation est respectée.
Se déplacer à haute vitesse étire les durées et comprime les distances (et donc réduit la vitesse perçue dans un autre référentiel). Cela demande un peu de réflexion, mais l’expérience montre la réalité de tout ça.
Facteur de Lorentz
Le taux d’étirement des durées ou de contraction des longueurs dépend de notre vitesse. Plus on s’approche de la vitesse de la lumière, plus l’effet est prononcé.
Ce taux est appelé le facteur de Lorentz, et il est noté γ (lettre grecque « gamma »). Il peut prendre toute valeur supérieure ou égale à 1.
Un facteur de Lorentz de 1,5 signifie que le temps s’écoule 50 % plus lentement pour les personnes dans un référentiel en déplacement, par rapport aux personnes dans un référentiel invariant.
Notons qu’un facteur γ de 1,5 s’obtient pour une vitesse de 75 % de celle de la lumière, et non pas 50 % : le facteur de Lorentz n’est pas linéaire par rapport à la vitesse de déplacement.
Typiquement, pour prendre un exemple : si l’on prend un chronomètre, que l’on voyage à 75 % de $c$ (donc 0,75c) pendant 1 h, et qu’on revient sur Terre, alors pour nous il se sera écoulé 1 h, mais sur Terre il se sera écoulé 1h30. Dit autrement, on a vieilli moins vite que ceux étant restés sur Terre. Si l’on exagérait, l’on dirait qu’on serait revenus jeunes sur Terre (ou du moins sans avoir vieilli) alors qu’eux auront largement vieilli) : c’est donc comme si on avait voyagé dans le futur !
(Note : je laisse totalement de côté ici les phénomènes décrits par le fameux paradoxe des jumeaux, ou autre. Il s’agit ici de simplifier, en ne considérant qu’un phénomène à la fois, dans un seul référentiel considéré à chaque fois aussi).
D’autres façons d’interpréter tout ça
La relativité chamboule beaucoup de choses. En plus de ce qui se trouve plus haut, on peut parler de l’énergie et de la masse des corps. Parmi ces choses, une chose dont vous avez déjà entendu parler : c’est le fameux E=mc².
Ce que cette équation indique, c’est que la masse m d’un corps correspond à une quantité d’énergie. Le rapport entre les deux étant la constante c — la vitesse de la lumière dans le vide — élevée au carré.
Pourquoi cette équivalence ?
Il faut arriver à voir que la masse d’un corps est une forme d’énergie comme une autre :
- La température d’un corps implique une énergie : l’énergie thermique ;
- La vitesse de déplacement d’un corps est une énergie : l’énergie cinétique (Ec) ;
- La masse, de même, est également une forme énergie : l’énergie de masse (Em). Dans l’équation d’Einstein, c’est cette énergie qui est également à mc² :
$$E_m = mc^2$$
Quand on est immobile, notre énergie cinétique est nulle. La seule énergie que l’on ait est notre énergie de masse. On dit que l’énergie de masse est l’énergie « au repos ».
Si l’on se déplace, on a en plus une énergie cinétique. Notre énergie totale est donc composée d’une énergie cinétique et d’une énergie de masse.
On peut alors se demander quel rapport de notre énergie est constituée par chacune des énergies. Si l’on fait ceci, on retombe sur le facteur de Lorentz :
$$\gamma = \frac{E_m + E_c}{E_m}$$
Avec ce raisonnement, on exprime notre énergie totale en fonction de notre énergie de masse au repos. Par exemple, si le facteur de Lorentz vaut 2, ça signifie que l’on a deux fois plus d’énergie que notre énergie de masse au repos. L’énergie cinétique Ec est égal à l’énergie de masse au repos Em.
Pour cet exemple, le facteur de Lorentz vaut 2 sur la vitesse de déplacement vaut 0,87c ! En voyageant à 87 % de la vitesse de la lumière, notre énergie cinétique devient égale à notre énergie de masse, et notre énergie totale devient le double de notre énergie au repos.
Cette « énergie totale » notée simplement E est appelée « énergie relativiste », et vaut γEm :
$$E = \gamma E_m = \gamma mc^2$$
On constate alors que plus γ augmente, plus notre énergie relativiste est important. De plus, notre énergie totale est proportionnelle à la masse : c’est donc comme si l’on multipliait notre masse à chaque fois que l’on multipliait notre γ.
Pour cette raison, parfois, on dit que notre masse augmente au fur et à mesure que l’on accélère : on parle alors de masse relativiste, ou masse apparente.
Exemples
Si l’on est immobile, notre énergie cinétique est nulle : toute notre énergie se trouve sous forme de masse. Le facteur de Lorentz vaut 1, l’écoulement du temps est normal et les distances ne sont pas contractées. On laisse de côté ce que ce « normal » signifie. Disons juste que son temps s’écoule comme d’habitude.
Si maintenant on voyage à 0,87c, le facteur de Lorentz vaut 2. Le temps s’écoule donc deux fois moins vite que pour quelqu’un qui ne se déplace pas. De plus, notre énergie cinétique atteint notre énergie de masse et notre énergie relativiste est le double de notre énergie de masse.
| Vitesse en km/s |
vitesse en % de c |
γ | % énergie sous forme d’énergie cinétique | |
|---|---|---|---|---|
| 0 km/s | 0 % | 1 | 0 % | |
| ~3 000 km/s | 1 % | 1,00005 | 0,0025 % | |
| ~30 000 km/s | 10 % | 1,005 | 0,25 % | |
| ~150 000 km/s | 50 % | 1,15 | 7,18 % | |
| ~260 000 km/s | 86,6 % | 2,00 | 33 % | |
| ~282 000 km/s | 94,3 % | 3,00 | 50 % | |
| ~297 000 km/s | 99 % | 7,09 | 75 % | |
| 299 493 km/s | 99,9 % | 22,4 | 91 % | |
| 299 762 km/s | 99,99 % | 70,7 | 97 % | |
| 299 789 km/s | 99,999 % | 223,6 | 99 % | |
| 299 792,458 km/s | 100 % | ∞ | 100 % (pas de masse) |
On constate alors que si l’on se déplace dans la dimension spatiale, le temps s’écoule moins vite. Et si l’on veut que le temps s’écoule normalement, on ne doit plus se déplacer.
On peut le résumer en disant « ce que l’on parcourt dans l’espace, on ne le parcourt plus dans le temps ».
Si l’espace s’écoule davantage (à cause de notre déplacement), alors le temps, lui, s’écoule au ralenti. Et inversement.
Implications
Avec le raisonnement précédent, plus on se donne de vitesse, plus l’énergie cinétique prend une part importante dans notre énergie relativiste, et donc plus γ augmente. Plus l’on se donne d’énergie cinétique, plus le temps s’écoule lentement et plus les distances deviennent grandes.
Malgré la difficulté de concevoir que l’écoulement du temps puisse varier, ceci implique d’autres bizarreries contre-intuitives, dont en voici quelques-unes.
- Premièrement, si l’on devait atteindre c, alors ça signifie que la totalité de notre énergie serait cinétique. Nous n’aurions que de l’énergie cinétique et aucune masse. Ce n’est pas pour rien que les photons, qui voyagent à la vitesse de la lumière, n’ont pas de masse du tout : toute leur énergie est cinétique. Leur masse au repos est nulle : c’est ce qui leur donne un γ infini et une impossibilité de voyager à une vitesse différente de c.
- Deuxièmement, en tentant d’atteindre c, on doit dépenser des quantités immenses d’énergie. D’un point de vue mathématique, si l’on vise la vitesse c, alors on doit acquérir une énergie infinie, même pour une masse minuscule. L’univers n’ayant (a priori) pas une quantité infinie d’énergie, c’est pour ça qu’on dit que la vitesse de la lumière ne peut pas être atteinte par un objet ayant une masse non nulle.
- Troisièmement, avec ce que j’ai dit plus haut à propos du facteur de Lorentz, plus on s’approche de la vitesse de la lumière, plus gamma augmente, et moins le temps s’écoule vite. Si l’on atteignait c, l’écoulement du temps s’arrêterait. C’est ce qui se passe dans le référentiel d’un photon. Le photon ne voit pas de temps passer. Même si dans notre référentiel le photon voyage durant des millions d’années, dans son référentiel à lui, il est absorbé au même instant qu’il est émis.
- Quatrièmement, on peut comprendre que si l’on allait au-delà de la vitesse de la lumière, alors le temps s’écoulerait plus lentement que zéro. C’est-à-dire qu’il reculerait, ce qui revient à dire que l’on remonterait le temps !
Si l’on pouvait voyager plus vite que la lumière, ça signifierait ni plus ni moins que l’on serait au point d’arrivée avant d’avoir quitté le point de départ.
De façon purement mathématique, si les équations de la relativité sont interdites pour une vitesse égale à la vitesse de la lumière, elles sont mathématiquement justes pour des vitesses supérieures à c. C’est simplement qu’elles impliquent que le temps s’écoule à l’envers. Mathématiquement ça se tient, même si physiquement c’est évidemment improbable. - Cinquièmement, une autre solution pour une vitesse supérieure à la lumière serait de ne pas toucher au signe du temps, mais d’inverser le signe de la masse. Si l’on a une masse négative, alors le facteur de Lorentz serait inversé aussi, et ça reviendrait — de fait — à voyager plus vite que la lumière. Ceci est souvent évoqué en science-fiction à propos des vaisseaux spatiaux : on parle ainsi d’avoir besoin d’une masse ou d’une énergie négative pour voyager plus vite que la lumière. Dans la pratique, ces choses n’ont jamais été observées (mais l’absence de preuve n’est pas une preuve de l’absence).
Conclusion
La relativité restreinte apporte l’idée selon laquelle l’espace et le temps sont malléables. Leur écoulement lorsque l’on se déplace (dans l’espace, mais aussi dans le temps) n’est pas le même en fonction de notre déplacement, comparativement à un référentiel qui serait resté immobile.
Ces choses-là ne sont pas un délire d’Einstein : ce sont des solutions mathématiques face à des observations de choses physiques bien réelles.
Les conséquences de ce changement de concept ne se font voir que pour des phénomènes extrêmes, en l’occurrence à de très hautes vitesses de déplacement (proches de celle de la lumière). C’est pour cela que la relativité est si récente, comparativement à la mécanique newtonienne : Newton, Galilée ou Kepler n’avaient pas les instruments ni les expériences pour voir que la physique classique qu’ils ont mise au point était fausse pour de hautes vitesses.
Il a fallu attendre Maxwell, Lorentz, Poincaré, Einstein… pour que ces phénomènes soient découverts, décrits mathématiquement, que des hypothèses soient posées et qu’une théorie entière et nouvelle soit construite.
Cet article n’est pas destiné à être un cours sur la relativité, mais plutôt de comprendre brièvement ce que c’est, et d’en voir quelques implications.
J’espère qu’il permet aussi de comprendre pourquoi la science-fiction parle parfois de « masse négative » ou « voyage dans le temps » en invoquant la relativité : ces choses-là se tiennent mathématiquement (même si les scénaristes simplifient généralement les choses pour ne parler que de ce point là). Les hypothèses nécessaires à tout ça n’ont simplement pas encore été validées par l’observation. Peut-être qu’un jour l’on observera (ou produira) une masse négative ou une vitesse supraluminique, ce qui ouvrirait alors la voie à des choses intéressantes.