
Cet article fait partie d’une série d’articles à l’occasion de la 26e CGPM (en 2018), à l’occasion de laquelle le kilogramme va être redéfini de façon historique et trois autre unités modifiées légèrement :
- Comment le kilogramme va être redéfini
- Pourquoi redéfinir le kilogramme ?
- Ampère, kelvin, mole : ce qui change, en plus du kilogramme (le présent article)
Comme expliqué dans les deux autres articles, le kilogramme va être redéfini : d’un artefact en alliage platine-iridium, on passe d’une définition basée sur la constante de Planck. Ce changement a lieu pour ne plus avoir de définition basé sur un objet (fragile et unique) mais sur une constante de la nature (infinie et éternelle).
L’une des conditions pour laquelle la nouvelle définition soit acceptée est une plus grande précision : la nouvelle définition doit être plus précise que l’ancienne.
Or, les unités ne sont pas toutes indépendantes : bien que des unités « de base », elles peuvent être liées les unes aux autres dans leur définition.
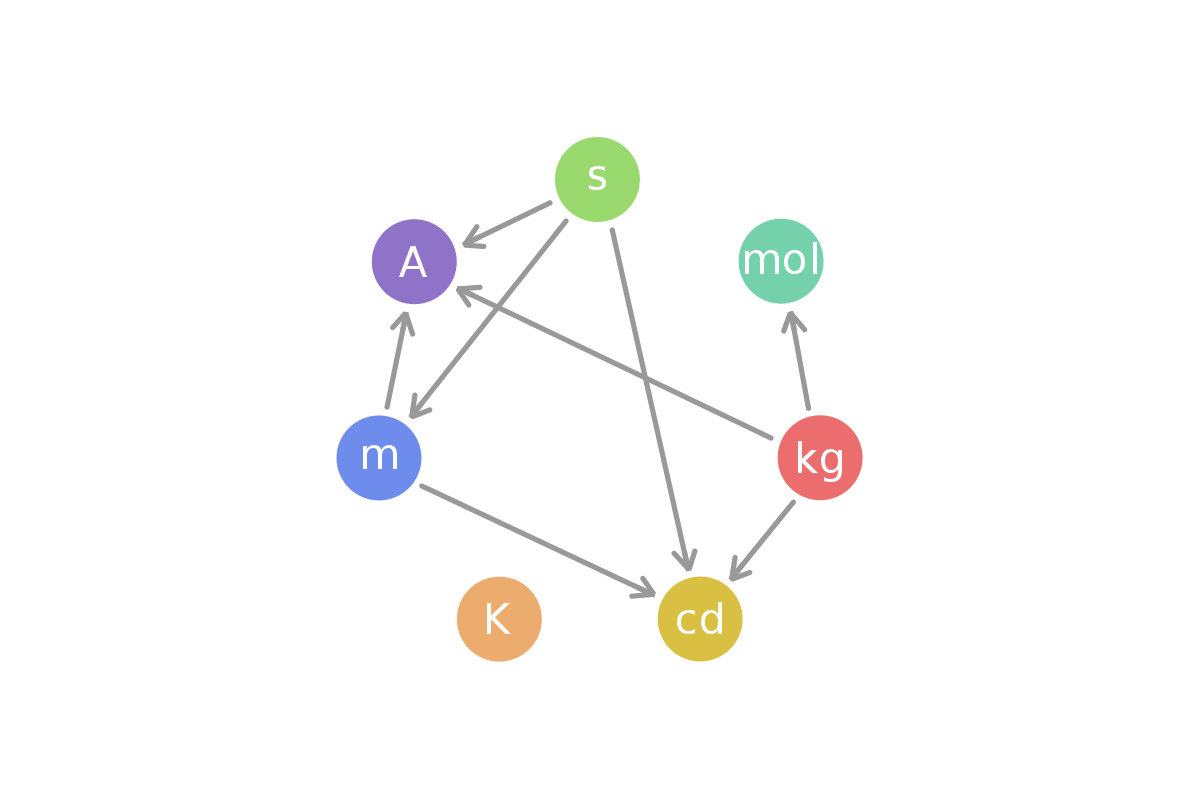
Ainsi, le mètre dépend de la vitesse de la lumière et de la seconde : toute incertitude sur la seconde se répercute dans une incertitude sur le mètre.
Si l’ancien kilogramme ne dépendait pas d’autres unités, le nouveau kilogramme, lui, dépend du mètre (et donc de la seconde). Par conséquent, les unités qui dépendaient de l’ancien kilogramme se voient désormais entachée d’une nouvelle incertitude sur le mètre et la seconde également.
Il fallait donc trouver une solution, et cela revient à trouver une nouvelle définition aux unités qui dépendaient du kilogramme, à savoir l’ampère, le kelvin et la mole.
Avec les nouvelles définition, qu’on va voir ici, tout ce jeu de dépendances est modifié :

Dans cet article, on va voir comment ces unités sont redéfinies, ce qui change et ce que ça implique, mais si vous avez compris le principe de redéfinition du kilogramme, vous comprendrez la redéfinition de ces autres unités : la méthode est identique.
Commençons par l’ampère.
L’ampère
L’ampère est l’unité du courant électrique : il définit non pas la vitesse des charges électrique en déplacement mais leur quantité traversant la section d’un fil électrique en un temps donné.
L’ancienne définition de l’ampère
Sa définition actuelle est la suivante :
Un ampère est l'intensité d'un courant constant qui, s'il est maintenu dans deux conducteurs linéaires et parallèles, de longueurs infinies, de sections négligeables et distants d'un mètre dans le vide, produit entre ces deux conducteurs une force linéaire égale à 2×10⁻⁷ newton par mètre.
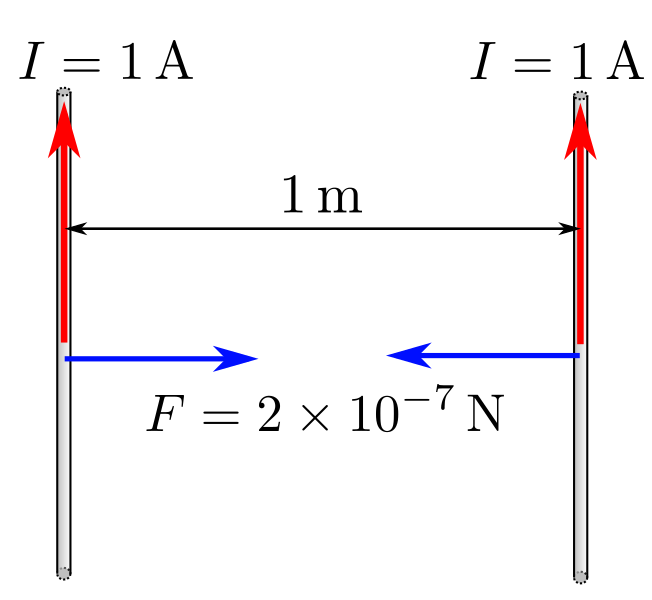
La dépendance de cette unité avec le kilogramme se trouve dans le terme de la force en Newton (qui est une unité dérivée). Aussi, cette unité est assez difficile à mettre mesurer en pratique : comment produire des fils de longueur infini ? Que signifie « négligeable » ?
Dans un mode où la précision est de rigueur, changer cette définition ne peut se faire que pour le mieux.
La nouvelle définition de l’ampère
Tout comme pour le kilogramme, la nouvelle définition va utiliser une constante physique : la charge de l’électron (ou du proton). Anciennement, cette constante était définie par (l’ancien) ampère et auquel on rattachait une incertitude liée à la mesure de l’ampère.
Désormais, on a fixé la valeur de la charge de l’électron et on va définir l’ampère grâce à elle. Sa nouvelle définition est devenue :
L'ampère, A, est l'unité du courant électrique ; sa valeur est définie en fixant la valeur numérique de la charge élémentaire à exactement $1,602\ 176\ 634 \times 10^{-19}$ quand elle est exprimée en ampère-seconde, ce qui correspond à des coulomb.
En d’autres termes, si un électron passe en une seconde à travers la section donnée d’un conducteur, on a une intensité de $1,602\ 176\ 634 \times 10^{-19}$ A (ce qui, pour obtenir un ampère, représente ~$6,241 \times 10^{18}$ électrons).
Cette définition reste assez facilement compréhensible : il suffit de faire passer un nombre connu d’électrons dans un fil en une seconde et on a l’ampère. Les autres redéfinitions, qui concernent le kelvin et la mole sont bien moins faciles à comprendre. Mais on va essayer.
Le kelvin
Le kelvin est l’unité légale de température thermodynamique.
La température thermodynamique correspond au degré d’agitation des molécules. Il n’y a rien de sorcier là dedans : quand on parle de la température qu’il fait dehors, c’est cette température là qu’on désigne.
L’agitation des molécules, quant à elle, correspond tout simplement à la vitesse moyenne de déplacement de ces molécules.
Comparée aux unités usuelles (Fahrenheit et Celsius surtout), elle est la seule qui commence au zéro absolu, c’est à dire la température la plus froide vers laquelle il est possible de tendre. Sur l’échelle en kelvin, il n’y a donc pas de températures négatives.
L’ancienne définition du kelvin
Jusqu’alors, l’échelle de température absolue était basée sur l’eau :
Le kelvin, unité de température thermodynamique, est la fraction $\frac{1}{273,16}$ de la température thermodynamique du point triple de l'eau.
À 0 °C à pression atmosphérique, l’eau peut se trouver à la fois sous la forme de glace et d’eau liquide : on trouve aussi bien de l’eau que de la glace à 0 °C.
À 100 °C à pression atmosphérique, l’eau peut se trouver à la fois sous la forme gazeuse et liquide.
Entre ces deux températures, l’eau est seulement liquide.
Le point triple, c’est un couple {pression, température} auquel un corps pur peut être à la fois liquide, solide et gazeux. C’est un point unique : chaque corps n’en a qu’un seul. Pour l’eau, cela correspond à 0,16 °C et 611 pascal.
Pour définir le kelvin, on prend la différence entre la température du point triple de l’eau et le zéro absolu, et on divise cette échelle en 273,16 graduations. Chaque graduation représente alors exactement 1 K.
Cette méthode est simple à comprendre et à obtenir, mais il faut tout de même avoir une eau très pure et de composition isotopique connue, chose qui, quand on requiert un certain degré de précision, commence à poser problème.
La nouvelle définition du kelvin
La nouvelle définition se veut plus précise et elle se base, encore une fois, sur une constante de la physique : la constante de Boltzmann. Cette constante est fondamentale à la thermodynamique, et relie un peu la thermodynamique macroscopique (échange de chaleur, fonctionnement d’un moteur thermique, etc.) et le monde microscopie (agitation et organisation des molécules, des atomes).
La nouvelle définition du kelvin s’énonce de la façon suivante :
Le kelvin, K, est l'unité thermodynamique de température ; sa valeur est définie en fixant la valeur numérique de la constante de Boltzmann à exactement $1,380\ 649 \times 10^{-23}$ quand elle est exprimée en s⁻²m²kgK⁻¹, ce qui correspond à des JK⁻¹.
Si on reprend notre histoire de vitesse de particules dans un gaz : la vitesse moyenne de déplacement des particules dans un gaz détermine la température de ce gaz.
La constante de Boltzmann se base sur le fait qu’à chaque mesure de vitesse moyenne d’une particule dans un gaz correspond une température précise.
La constante de Boltzmann, c’est la quantité d’énergie cinétique qu’une particule dans gaz gagne quand sa température grimpe de 1 kelvin. Ainsi, pour chaque kelvin gagné, l’énergie cinétique augmente de $1,380\ 649 \times 10^{-23}$ joule.
En ayant fixée la constante de Boltzmann, et en sachant mesurer très précisément la température, on détermine ce à quoi correspond 1 kelvin.
En pratique, les mesures ont été faites à l'aide d'un résonateur acoustique à gaz : une enceinte remplie d'un gaz et dans laquelle on mesure la vitesse de propagation d'un son émis à la résonance de l'enceinte, ce dernier dépendant de la température (voir).
En notant la vitesse du son à la température du point triple de l'eau, on arrive à remonter à la température microscopique des molécules et donc à la valeur de la constante de Boltzmann. Ensuite, comme pour les autres unités, on fixe la constante une fois pour toute et l'on peut l'utiliser pour déterminer la température, inversant le sens du problème.
La constante de Boltzmann peut aussi être appliquée à un ensemble de particules. Si on l’applique à une mole de particules gazeuses, alors l’énergie gagnée par l’ensemble de ces particules quand on augmente leur température de 1 K est de 8,314 459 8 joules, valeur notée par $R$ et dénommée constante des gaz parfaits.
En d’autres termes, la constante de Boltzmann et la constante des gaz parfaits sont liées par la mole, qui est la dernière unité à être redéfinie.
La mole
Tout comme une douzaine de particules correspond à 12 particules, on a une mole de particules qui correspond à $6,022\ 140\ 76 \times 10^{23}$ particules.
Pourquoi cette quantité de particules en particulier et pas une autre ? Cela provient de son ancienne définition.
L’ancienne définition de la mole
L’ancienne définition va comme suit :
La mole est la quantité de matière d'un système contenant autant d'entités élémentaires qu'il y a d'atomes dans 0,012 kilogramme de carbone 12
Il a été choisit le carbone 12 parce qu’il fallait un élément connu et facile à obtenir. De façon approximative, la mole correspond au nombre de particules se trouvant dans $n$ grammes d’un élément de masse atomique $n$. Donc dans 1 gramme d’hydrogène, 4 grammes d’hélium 4 ou 12 grammes de carbone 12.
La nouvelle définition de la mole
La nouvelle définition est assez simple vu qu’elle correspond juste à la définition du nombre d’Avogadro :
La mole, mol, est l'unité de quantité de matière d'une entité élémentaire spécifique, qui peut être un atome, une molécule, un ion, un électron ou n'importe quelle autre particule ou groupe particulier de ces particules ; sa valeur est définie en fixant la valeur numérique du nombre d'Avogadro à exactement $6,022\ 140\ 76 \times 10^{23}$ quand elle est exprimée en mol⁻¹.
En fait, une mole c’est juste « le nombre d’Avogadro » particules.
Ça semble un peu bête qu’il faille une unité pour ça (c’est d’ailleurs un reproche qu’on fait à cette grandeur : c’est juste un nombre sans réelle signification physique), mais cette valeur est suffisamment intriquée aux autres unités pour que le BIPM juge nécessaire de l’intégrer avec elles.
Certains diront que l’on dispose ainsi de 7 unités, qui a toujours été un nombre « mystique ».
Et les autres unités ?
Les autres unités, que sont la seconde, le mètre et la candela (pour la mesure d’une durée, d’une distance et d’une intensité lumineuse) n’ont pas eu leur définition fondamentalement révisée. Elles sont simplement reformulées, afin que les sept unités de base aient des définitions suivant le même schéma :
La seconde :
La seconde, s, est l'unité de durée ; sa valeur est définie en fixant la valeur du nombre de périodes de la radiation correspondant à la transition entre les deux niveaux hyperfins de l'état fondamental de l'atome de césium 133 à la température du zéro absolu à exactement 9 192 631 770 quand elle est exprimée en s⁻¹
C’est donc toujours la durée nécessaire pour avoir 9 192 631 770 périodes d’oscillation d’une radiation précise de l’atome de césium 133.
Le mètre :
Le mètre, m, est l'unité de longueur ; sa valeur est définie en fixant la valeur de la vitesse de la lumière dans le vide à exactement 299 792 458 quand elle est exprimée en m s⁻¹
Il s’agit toujours de la distance parcourue par la lumière en une fraction $\frac{1}{299\ 792\ 458}$ de seconde dans le vide.
La candela :
La candela, cd, est l'unité d'intensité lumineuse dans une direction donnée ; sa valeur est définie en fixant la valeur numérique de l'intensité énergétique d'un rayonnement monochromatique de fréquence $540 \times 10^{12}$ s⁻¹ (hertz) à exactement 683 quand elle est exprimée en s³⋅m⁻²⋅kg⁻¹⋅cd⋅sr, ou cd⋅sr⋅W⁻¹, ce qui correspond à des lm⋅W⁻¹.
En gros, une lumière verte (de 540 THz) qui émet $\frac{1}{683}$ watt par stéradian (un angle solide, un cône en quelque sorte) a une intensité lumineuse de 1 candela. Là aussi, celle définition est la même qu’avant.
Pour conclure
Nos 7 unités de base sont maintenant toutes définies à partir d’une constante de la physique (vitesse de la lumière, charge de l’électron, quanta d’énergie (Planck, Boltzmann)…). Ces constantes sont aujourd’hui toutes fixées à une valeur précise et ce sont les unités qui en dépendent désormais.
De plus, chaque unité dispose aujourd’hui d’une définition dont l’énoncé suit une structure identique à chaque fois (ce qui peut simplifier leur apprentissage). Je trouve néanmoins que ces définitions, même si plus simples à apprendre, sont plus compliquées à comprendre.