
Quand on manipule les nombres, et ce depuis d’école, on les classe en différentes catégories, différents ensembles. Ce sont les ensembles de nombres, bien connus :
- ℕ : les nombres naturels ;
- ℤ : les nombres relatifs ;
- 𝔻 : les nombres décimaux ;
- ℚ : les nombres rationnels ;
- ℝ : les nombres réels ;
Et bien-sûr :
- ℂ : les nombres complexes.
Ces ensembles ne sortent pas de nulle part, et chacun a été inventé pour répondre à des problèmes précis. Si bien qu’aujourd’hui, les nombres naturels, relatifs, décimaux… font partie de la vie courante.
Les nombres complexes sont encore un peu à part, car ils semblent si étranges : « des racines de nombres négatives ?! Et puis quoi encore ? ».
Pourtant, il fut un temps où l’on aurait pu se dire la même chose des nombres négatifs ou à virgule, qui sont tout aussi absurdes si l’on ne connaît que les nombres naturels : « des nombres plus petits que zéro ?! », « des nombres pas entiers ?! »
Cet article a pour but de démystifier les nombres complexes, de revenir sur leur origine et de parler de leur utilité.
Pour cela, je vais d’abord revenir sur les autres ensembles. Cela permettra de mettre en évidence le fait que chacun ensemble résout un problème que les ensembles « inférieurs » ne peuvent pas résoudre.
On remontera ainsi jusqu’à l’ensemble ℂ… voire, au delà !
Les ensembles de nombres
Les nombres naturels, ℕ
Au cours de notre enseignement, à la plus petite école, pour ce qui est des nombres, on apprend tout d’abord des nombres naturels : 0, 1, 2, 3, etc.
Ce sont les nombres entiers et positifs. On peut s’en servir pour dénombrer des choses, comme des biscuits, des pièces d’or, des chèvres…
On peut tout à fait représenter ces nombres sur un axe croissant :
![]()
Quand on dit à un enfant de 5 ans de compter, ce sont les nombres qu’il récitera. C’est la façon la plus naturelle de dénombrer des choses, d’où leur nom. Pour un enfant, ces nombres sont les seuls qui existent et représentent tout ce qu’il y a à savoir.
Les nombres relatifs, ℤ
Historiquement, avec le commerce est apparu la notion d’addition et de soustractions : si l’on possède 5 chèvres et qu’on en vend 2, il nous en reste 3. De façon mathématique, ça revient à faire 5−2=3.
Maintenant, que se passe-t-il si nous avons 2 chèvres et qu’on en vend 5 ? Ce n’est pas possible ! C’est une escroquerie !
En effet, si l’on n’a que des nombres naturels, il est impossible de faire 2 moins 5 : cinq est plus grand que deux, donc les soustraire est… absurde..
C’est d’ailleurs ce qu’on enseigne à l’école primaire : on ne peut pas soustraire un grand nombre d’un plus petit.
Pourtant, de façon abstraite et d’un point de vue purement mathématique, un nombre est un nombre, donc on devrait pour les commuter sans problème. On a inventé les nombres relatifs pour permettre cette opération absurde qui est retirer un grand nombre à un plus petit.
Un nombre qui serait ainsi inférieur au néant serait noté avec signe « − » devant. Comme ceci : « −3 ».
Mentalement, une abstraction est nécessaire pour parvenir à comprendre les nombres négatifs. Si l’on parle de chèvres ou de pommes, on ne peut pas. Mais si l’on dissocie les mathématiques du monde réel, que l’on considère seulement les mathématiques comme une discipline abstraite, alors oui, on peut faire tout ça : après tout, les maths n’ont pas de limites.
Résultat ? Avec les nombres relatifs, soustraire des nombres peut se faire dans n’importe quel sens : 2−5=−3 !
Est-ce qu’on peut utiliser ça pour des chèvres ? Probablement pas. Mais on peut s’en servir pour des impôts, et pour constater que notre solde est négatif, ou positif, et donc savoir qui doit des pièces d’or à qui.
On parle des nombres relatifs, car ils n’ont de signification que par rapport à d’autres : −3 pommes n’a pas de sens dans l’absolu, mais « 5 pommes − 3 pommes » a du sens si l’on considère un ensemble de cinq pommes dont on en en mange trois. Les trois pommes sont considérées relativement à notre capital de cinq pommes.
Sur l’axe des nombres, ces nombres sont de l’autre côté de l’origine :
![]()
Bien-sûr, avec ces nouveaux nombres, il a fallu établir de nouvelles règles de calcul. Par exemple, la multiplication de deux nombres négatifs donne un nombre positif : c’est le fameux « − par − égale + ».
De plus, enfin, il a fallu établi une notation particulière : ainsi, un nombre plus petit que zéro s’écrit avec un signe « − » devant. Trivial pour vous ou moi, mais c’est important.
Les nombres décimaux, 𝔻
On peut aller plus loin : pour l’instant, les nombres sont certes sur un axe et organisés, mais il y a de l’espace entre chaque nombre. Qui a-t-il entre 1 et 2 ?
Posée dans le cadre des ensembles ℕ ou ℤ, cette question n’a pas de sens : il n’a rien entre 0 et 1. Il n’y a rien entre 1 chèvre et 2 chèvres !
Cette notion n’est pas utile avec des chèvres, mais peut l’être, par exemple, avec un gâteau.
Un gâteau ne se mange que rarement en entier : on s’en coupe une partie. Si l’on mange la moitié du gâteau, il nous en reste une partie située exactement entre 0 gâteau et 1 gâteau. Pour ces cas-là, on a inventé les nombres décimaux, capables, eux, de représenter des morceaux de partie entière.
Avec la notation à virgule, on note cette quantité « 0,5 gâteau », où l’on considère la distance entre 0 et 1 comme une unité divisible en 10 fractions d’un dixième chacun et l’on récupère cinq de ces dixièmes. C’est pourquoi ces nombres sont appelés « nombres décimaux ».
Au passage, on divise en 10 car nous utilisons la base 10 pour compter. Ce serait une autre histoire en base 2 binaire par exemple.
Sur notre axe des nombres, les décimaux sont notés entre les entiers.
![]()
Pour l’instant je ne vous apprends rien. Mais il faut bien comprendre qu’à chaque nouvel ensemble de nombre, on répond à un problème que l’ensemble précédent ne gère pas. On trouve alors un mécanisme mathématique pour solutionner ça. On y ajouter une notation particulière, et quelques règles arithmétiques et nous voilà avec un nouvel ensemble.
Les nombres rationnels, ℚ
Reprenons notre exemple avec les parts de gâteau. On sait noter une moitié de gâteau, et même un quart.
Maintenant, comment noter un morceau du gâteau coupé en 3 parts égales ? Nous aurions eu 0,333333333… gâteau, avec une infinité de « 3 ». Ce nombre, sous cette forme, ne peut pas être écrit sans une notation particulière : il nous faudrait une infinité de papier et d’encre, ce qui est impossible.
Pourtant, notre part de gâteau existe bien : elle reste possible, même si l’écrire ne l’est pas.
On constate alors que l’on possède 1 gâteau que l’on a divisé en 3. On va donc utiliser la notation « 1/3 ».
Sous cette forme, on rapporte notre part de gâteau comme un ratio du gâteau entier. On les appelle donc les nombres « rationnels ».
Ces nombres regroupent tous les nombres qu’il est possible d’écrire sous une forme de ratio de deux nombres entiers relatifs : 1/2, −1/3, 1/7, 1/1, 2/1…
Ils réussissent là où les nombres à virgule montrent leur limite : 0,33 gâteau est une valeur approchée du tiers d’un gâteau, mais « 1/3 » en est une valeur exacte.
Là aussi, ils se mettent bien sur l’axe des nombres :

(Note : 0,33333… à l’infini, est parfois noté aussi « 0,3 », où le 3 signifie « "3" répété à l’infini »).
Les nombres réels, ℝ
Notre axe des nombres contient maintenant les nombres naturels, les entiers relatifs, décimaux, rationnels… Y en a-t-il d’autres ? Oui : $\pi$ (« pi ») en est un exemple très connu.
$\pi$ ne peut pas être écrit sous la forme d’une fraction de deux nombres relatifs. Il n’appartient donc pas aux nombres rationnels : il est irrationnel. L’ensemble qui regroupe les rationnels et les irrationnels est l’ensemble des réels.
Les nombres réels se définissent comme pouvant être écrits avec une partie entière suivie ou non d’un nombre fini ou infini de décimales. Ceci inclut donc les autres ensembles vus jusqu’ici, ainsi que les nombres tels que Pi.
On peut placer Pi sur l’axe des nombres : on sait qu’il se trouve quelque part entre 3 et 4 :

$\pi$ et$\sqrt{2}$ (la racine carrée de deux) sont des réels irrationnels. $\phi$ (phi, le nombre d’or), ℯ (la constante de Neper) en sont deux autres très connus, et il y en a d’autres que je n’énumérerais pas tous.
Relations entre ces ensembles
On l’a vu : les nombres naturels font partie des nombres relatifs : ils sont inclus dedans. De même, les nombres entiers et relatifs font partie des nombres décimaux : le nombre 2 peut être écrit 2,0.
Il peut aussi être écrit 2/1 : il est donc également contenu dans les nombres rationnels. Enfin, il se trouve également dans les réels.
On peut donc établir que les ensembles sont contenus les uns dans les autres :

Toutes les mathématiques que l’on apprend au collège, ainsi que tout ce qu’on fait « dans la vie courante » concerne les nombres réels. Ceci nous suffit pour la vie courante.
Et du coup, 𝑖 et ℂ ?
Un esprit curieux peut se demander s’il existe d’autre chose que les réels.
Ces derniers sont sur un axe, qui est l’axe des réels. Existe-t-il des nombres en dehors de cet axe ? La réponse à cette question : et pourquoi donc pas ?
Comme ceci :
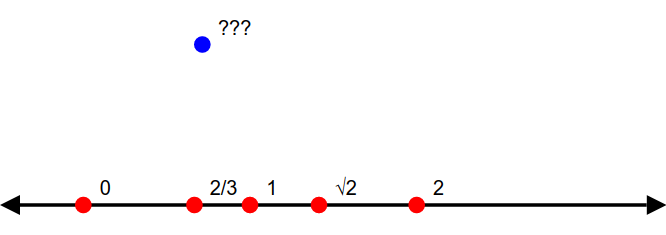
Si l’on peut l’imaginer, alors on peut le créer. En a-t-on vraiment besoin ? Et bien… oui, il se trouve.
Du besoin d’un nouvel ensemble
Comme expliqué plus haut, les ensembles sont créés en fonction des besoins. Lorsqu’un ensemble ne suffit pas à faire ce qu’on fait, on peut-être amené à créer un ensemble plus vaste. L’invention d’un nouvel ensemble fait donc suite à un problème face auquel on disait « nope, c’est impossible ! ».
Pour l’ensemble des nombres imaginaires, la démarche est identique. Historiquement, on faisait face à un problème lié aux polynômes et leurs racines (les polynômes sont un type d’équations et les racines en sont les solutions).
À l’époque de la découverte des polynômes, au XVIᵉ siècle, l’hypothèse fut posée qu’un polynôme non-constant de degré N admet toujours N solutions. C’est un théorème très important, connu aujourd’hui sous le nom de théorème fondamental de l’algèbre.
Dans la recherche de ces racines, certaines n’avaient aucun sens : elles faisaient intervenir des carrés négatifs ! Or ceci est impossible : un nombre réel élevé au carré est toujours positif. L’on fut donc dans cette situation devant laquelle on dit « nope c’est impossible ! ».
Pour contourner ce problème, il fut alors inventé un ensemble de nombres n’appartenant pas aux réels (et donc en dehors de l’axe des nombres réels), et pour lesquelles on pourrait avoir des racines négatives.
Ces nombres furent appelés « irréels » ou « impossibles ». René Descartes les appela « nombres imaginaires », qui est le terme qui est resté aujourd’hui.
Tout comme on a dû inventer le signe « − » des nombres relatifs, ou la virgule « , » des nombres décimaux, on a inventé un symbole pour représenter un nombre dont le carré est négatif. Ce symbole, c’est « 𝑖 », et l’ensemble de nombres qui comprennent 𝑖 est appelé « ensemble des nombres complexes », noté ℂ :

Définition de 𝑖
La définition est assez bête : 𝑖 est un symbole qui, juxtaposé à un nombre, lui confère la propriété de donner un carré négatif.
Par exemple, les nombres 2𝑖, 3𝑖, ou x𝑖, deviennent négatifs quand on les élève au carré : respectivement −4, −9 et −x².
𝑖 est tout simplement un symbole qui ajoute un sens particulier à un nombre. En fait, 𝑖 est lui-même un nombre. Il est défini de façon à vérifier l’équation :
$$i^2 = -1$$
Au sein des réels, si l’on met un nombre au carré, il est forcément positif.
Avec les nombres imaginaires, un carré négatif devient possible s’il contient 𝑖.
Par exemple, si l’on a l’équation x²=−4, alors les solutions sont 2𝑖 et −2𝑖. En effet, si l’on calcule les carrés de 2𝑖 et −2𝑖, on retombe bien sur −4 dans les deux cas.
D’où il sort ? De la nécessité de pouvoir faire des calculs impossibles dans ℝ.
Tout comme le signe « − » est sorti de la nécessité de faire des calculs avec des nombres qui n’existaient pas avant. Avant le signe « − », il était impossible de soustraire 5 à 2, mais avec le les nombres relatifs et leur signe « − », on décide que l’on peut quand-même le faire.
Imaginaires purs et nombres complexes
Un nombre qui comporte le signe 𝑖 est dit imaginaire : 2𝑖 est un imaginaire. Il est même dit « imaginaire pur ».
En effet, il existe des imaginaires qui ne sont pas purs. Ils sont dits complexes.
Un tel nombre est par exemple « 2𝑖 + 4 ». Ceci est bien un seul nombre, pas deux.
Il est dit « complexe » car composé de deux parties (le « complexe » est donc à prendre au sens populaire) :
- 2𝑖 : sa partie imaginaire (elle-même composée de 2, un réel, et de 𝑖, l’unité imaginaire) ;
- 4 : sa partie réelle.
Ici, quand on dit « partie réelle » on fait référence à la partie qui n’a pas de 𝑖, et qui tombe donc dans l’ensemble des nombres réels.
De façon générale, tout nombre complexe noté z est de la forme :
$$z = a+ib$$
Où a et b sont des réels, qui peuvent éventuellement être nuls. Car il ne faut pas oublier que l’ensemble des nombres complexes englobe l’ensemble des nombres réels. Tout nombre réel est complexe, c’est juste que sa partie imaginaire s’écrit « 0𝑖 », donc 0, donc on ne l’écrit pas. Un peu comme un entier est un nombre décimal : on peut écrire 1 sous la forme 1,0. C’est juste qu’on écrit simplement 1. C’est la même démarche.
Plan complexe
Vous vous souvenez de l’axe des nombres ? Au début on avait les nombres naturels : 1, 2, 3… que l’on plaçait à la suite sur un axe qui démarre à 0. Puis on a étendu l’axe au-delà de 0, pour y mettre les négatifs. Puis on a commencé à écrire des nombres entre les entiers, comme 3,2 ou 1,54, puis pour les rationnels et les irrationnels.
Les nombres complexes ne font pas partie des réels : ils ne se mettent pas sur cet axe. Ils doivent donc se trouver ailleurs. Or, si l’on est en dehors de l’axe, on se trouve… dans un plan ! Ce plan contient deux dimensions : on parle alors du plan complexe.
Un point du plan est repéré par son abscisse et son ordonnée : l’abscisse est sa position le long de l’axe des réels, et correspond à sa partie réelle. L’ordonnée est sa position le long de l’autre axe, l’axe des imaginaires :
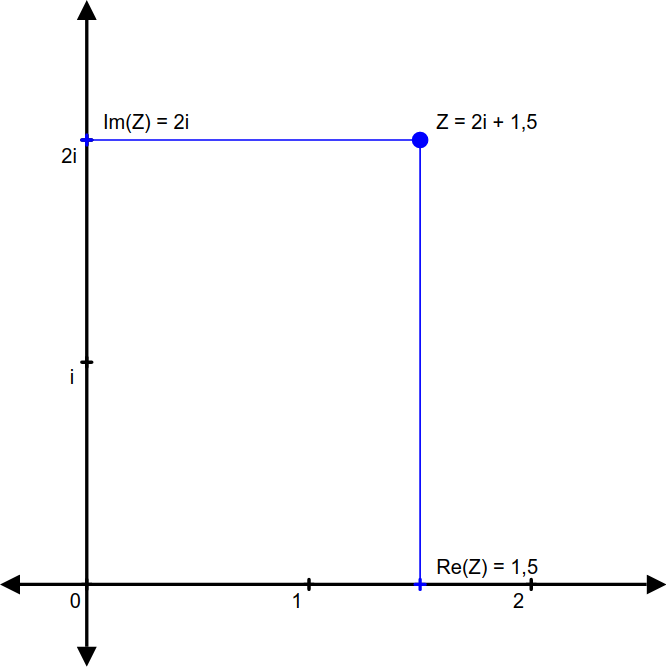
On remarque alors que si un nombre a une partie imaginaire nulle, il se retrouve sur l’axe des réels. Inversement, un nombre avec une partie réelle nulle se retrouve sur l’axe des imaginaires, et c’est alors un imaginaire pur.
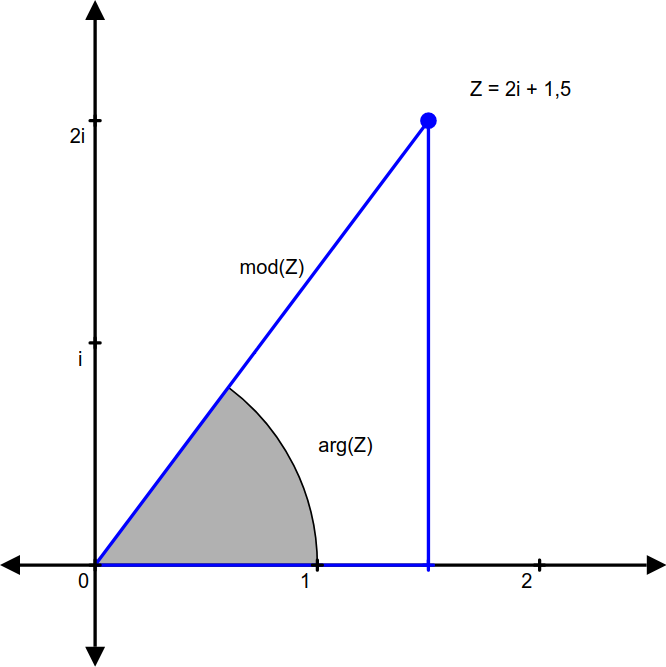
Une chose intéressante quand on a un point Z dans ce plan complexe, c’est qu’on peut tracer un triangle rectangle avec ce point comme un des sommets et l’origine O du repère comme un autre sommet.
La distance de ce point Z à l’origine O se calcule avec le théorème de Pythagore en considérant le triangle dont ZO est l’hypoténuse. Les deux autres côtés mis au carré donnent le carré de l’hypoténuse :
$$mod(Z) = |Z| = \sqrt{\operatorname{Im(Z)}^2 + \operatorname{Re(Z)}^2}$$
Cette distance est appelé le module du nombre complexe Z. L’angle du vecteur OZ par rapport à l’axe des réels est quant à lui appelé l’argument du nombre complexe.
L’argument et le module constituent les coordonnées polaires du point complexe dans le plan complexe, ce qui est parfois plus utile qu’utiliser les coordonnées cartésiennes :
Autres formes d’un nombre complexe : forme trigonométrique et forme exponentielle
L’on vient ici de relier les angles — et donc la trigonométrie — aux nombres complexes. Ces choses donnent lieu à des calculs trigonométriques sur des nombres complexes. Les fonctions trigonométriques peuvent s’appliquer aux nombres complexes et cela crée de nouvelles propriétés.
Par exemple, le cosinus de l’argument d’un nombre complexe correspond à sa partie réelle, et le sinus de l’argument est sa partie imaginaire. Si notre nombre complexe est $z = a + ib$, alors on a :
$$a = \mod(z) \times \cos(\arg(z)) \\ b = \mod(z) \times \sin(\arg(z))$$
Si l’on note θ, (théta) son argument, et ρ (rho) son module, alors l’écriture précédente devient :
$$a = \rho \times \cos(\theta) \\ b = \rho \times \sin(\theta)$$
Et donc, en remplaçant a et b dans l’écrire z = ai+b, cela devient :
$$z = \rho \cdot \lbrack \cos(\theta) + i \sin(\theta) \rbrack$$
Sous cette forme, on peut utiliser toutes les formules de trigonométrie usuelle, comme les formules bien connues d’additions d’angles (les fameuses « coco-sisi » et « sico-cosi »), les formules de Simpson ou de Moivre, ou encore les formules de duplication. On remarque aussi la périodicité $2\pi$ des nombres complexes.
On peut également faire intervenir des fonctions exponentielles dans tout ça, considérant la formule d’Euler qui lie l’exponentielle aux fonctions trigonométriques:
$$\cos(z) = \frac{e^{iz} + e^{-iz}}{2} \\ \sin(z) = \frac{e^{iz} - e^{-iz}}{2i}$$
Après arrangement des termes dans l’écriture trigonométrique :
$$e^{i\theta} = \cos(\theta) + i \sin(\theta)$$
Ce qui peut s’écrire finalement sous sa forme exponentielle :
$$z = \rho e^{i\theta}$$
L’exponentielle complexe conserve sa propriété de transformer les sommes en produits, ce qui, à nouveau, peut être utile dans certains cas de figures.
En particulier, le produit i×i qui vaut −1, et que l’on peut alors démontrer très facilement. Soit le nombre complexe ζ (zeta) = a+𝑖b, où a=0 et b=1. ζ=𝑖 est donc imaginaire pur. De plus, son module vaut 1 et son argument vaut 90°, ou π/2. Mettons ça sous sa forme exponentielle :
$$\zeta = i = 1 e^{i\frac{\pi}{2}}$$
Donc :
$$\begin{aligned}\zeta^2 = i^2 &= (e^{i\frac{\pi}{2}})^2 \\ &= e^{i\pi}\end{aligned}$$
Notre nombre ζ² a donc pour module toujours 1 et pour argument π. Or, l’argument est un angle, et un angle de π, sur le cercle trigonométrique a pour sinus −1 et pour cosinus 0. Le sinus étant la partie réelle du nombre complexe, et le cosinus sa partie imaginaire, l’écriture de ζ² devient ζ² = 0𝑖−1 soit ζ²=−1, soit :
$$\zeta^2 = i^2 = -1$$
Dans le plan complexe, ζ² se place à un angle de 180°, donc à gauche de l’origine sur l’axe des réels, autrement dit, dans les réels négatifs. On retrouve donc ce résultat de façon géométrique aussi. CQFD.
Enfin, ceci donne lieu également à l’une des plus belles équations des mathématiques, l’identité d’Euler :
$$\text{e}^{\text{i}\pi} + 1 = 0$$
Et en physique ?
Tout ceci sert à quoi ?
La trigonométrie, les sinusoïdes pour commencer, est fortement liée aux phénomènes alternatifs comme les courants électriques ou les oscillations d’un ressort ou d’un pendule. On peut décrire ces phénomènes en utilisant le plan complexe et donc 𝑖, et c’est généralement ce que l’on fait. Ainsi, plutôt que de dessiner une sinusoïde comme on en a l’habitude, on utilise un plan complexe et le cercle trigonométrique.
Le cercle correspond alors à la trajectoire d’un point qui évolue en X et Y (cela revient au même que la trigonométrie : la projection Z du X sur le cercle a pour Y le cosinus de l’angle OZ, mais les calculs se font alors dans un autre formalisme — je passe les détails car ça sort un peu du cadre de l’article).
Comme les dérivées, les nombres complexes ne sont pas un délire de matheux mais voient des applications dans la réalité et le monde physique.
Les phénomènes physiques décrits avec des nombres complexes ne sont pas rares en physique : c’est le cas par exemple des oscillateurs harmoniques, des phénomènes périodiques, de l’électromagnétisme, l’électricité de puissance, des ondes, et donc aussi à tout ce qui touche à la transmission de données (fibres optiques, ondes radio, encodage de données…).
Plus compliqué : en relativité et en physique quantique, l’espace et le temps peuvent constituer un plan complexe. Encore plus fort, on peut se retrouve avec choses comme des temps imaginaires, situés ni dans le passé, ni dans le futur, mais sur un axe différent du nôtre. Stephen Hawking, qui l’a largement popularisé dans ses travaux, en dira :
Le temps imaginaire est la seule partie de mon travail que les auteurs de science-fiction n’ont pas utilisé, car ils ne le comprennent pas.
— Stephen Hawking
Ça demande en effet une certaine capacité d’abstraction pour réussir à en saisir le sens, mais dans certains modèles théoriques, ces choses semblent fonctionner pour modéliser la réalité.
En conclusion
Pour les nombres complexe, il faut surtout retenir qu’ils brisent certaines règles des nombres réels : c’est précisément leur but ! Ils sont là pour faire ce que les règles des nombres réels empêchent de faire sur les réels. Donc a crée un cadre plus vaste. C’est comme les nombres relatifs qui brisent des règles des nombres naturels : dans les relatifs, on peut ainsi aller plus bas que zéro.
Le terme « complexes » ne doit pas faire peur. On aurait pu dire « nombres en 2D », ça serait revenu au même, car ils ont deux dimensions, sur le plan complexe, plutôt que la droite des réels.
Quant à 𝑖, il s’agit juste d’un symbole. Un symbole qui confère à un nombre la caractéristique de donner un carré négatif. C’est un symbole au même titre que le signe « − » ou la virgule du décimal. C’est juste qu’ici, 𝑖 est lui-même un nombre.
La encore, le terme « nombre imaginaire » est juste une terminologie mal choisie. Tous les nombres sont imaginables, comme ils sont tous vrais et existant. On aurait pu dire que ce sont des nombres « subréells » ou « planéiques », car ils ne sont pas sur l’axe des réels et ont besoin d’un plan pour être représentés. Mais le fait qu’ils soient qualifiés d’imaginaires ne doit pas laisser penser que ce sont des nombres que l’on ne peut qu’imaginer : ils sont là, pour de vrai, et ont leur propres règles, plus larges que les autres nombres (les réels).
Pour finir, une grande question :
Y a-t-il quelque chose au-delà des imaginaires et de l’ensemble ℂ ?
Bien-sûr ! Sur le même principe d’extension d’un ensemble vers un autre aux propriétés plus permissives (et en utilisant des unités plus larges que 𝑖), il existe l’ensemble des quaternions (noté ℍ).
Ils font intervenir des unités comme 𝑖, 𝑗 et 𝑘, avec des propriétés propres et a priori sortis d’un chapeau. Mais encore une fois, ce n’est pas plus étrange qu’un nombre négatif.
Au-delà, des quaternions, on trouve ensuite l’ensemble des octonions (𝕆), des sédénions (𝕊) et plus largement les ensembles de 2n dimensions (en fait ℝ, ℂ, ℍ, 𝕆 et 𝕊 sont respectivement les dimensions 1, 2, 4, 8 et 16 des nombres réels).
Tous ces ensembles, au-delà des complexes sont dits hypercomplexes, et peuvent trouver des applications également.