
Quand on souhaite transmettre une information, il y a plusieurs façons de procéder. On peut transmettre l’information elle-même directement, ou alors une description plus ou moins précise de l’information.
Par exemple, si j’ai un plat cuisiné et que je veux faire goûter ça à quelqu’un, je peux :
- prendre le plat et l’envoyer directement à mon correspondant ;
- ou bien dire au correspondant comment reproduire le plat, donc en lui communiquant sa recette.
Dans le premier cas, on envoie le plat directement. Cette méthode est fiable mais lente : elle nécessite un transport spécial par la Poste. On ne peut transmettre un plat ni par e-mail ni au téléphone avec la parole.
Dans le second cas, on envoie toutes les informations nécessaires pour reproduire le plat. Ça n’est pas le plat directement, mais avec le bon matériel on peut reproduire le plat. Cette méthode a l’avantage de pouvoir être transmise très rapidement à notre correspondant : par courrier, e-mail, oralement… Seul souci, il faut que le correspondant sache cuisiner et ait les denrées et le matériel nécessaire.
En informatique et en traitement du signal, il est intéressant de pouvoir faire pareil. Un signal sonore d’une musique où l’on envoie chaque point du signal sonore à la suite (signal non compressé, sans perte, ou « lossless ») prend plus de place qu’une description mathématique de ce signal.
Or, en informatique et en transfert réseau, la place ça coûte cher et il faut en réduire la consommation. On utilise donc des méthodes pour transmettre la même chose mais avec moins de données.
En pratique pour un fichier sonore, on peut utiliser ce qu’on appelle la décomposition en séries de Fourrier : un principe mathématique fait pour transformer un signal quelconque en un modèle mathématique et logique, nettement moins lourd.
Principe de base
Notre fichier musical brut et sans pertes pèse trop lourd. On utilise donc un format, le MP3 par exemple, pour le compresser. Le MP3 utilise la décomposition en séries de Fourrier.
Ce que Joseph Fourrier a dit, au travers de ses concepts mathématiques, c’est que n’importe quel signal compliqué (comme la voix ou une chanson) peut être décomposé en une somme de signaux beaucoup plus simples (des sinusoïdes simples, en l’occurrence).
Pour voir comment ça fonctionne, voyons une analogie. Imaginons que nous ayons un cercle sur le sol que l’on doit recouvrir avec des carreaux de faïence carrés.
Ce qu’on va faire, c’est commencer par mettre le plus grand carré possible que l’on peut placer dans le cercle. Ensuite, on va mettre des carrés plus petits dans les coins, puis des carrés encore plus petits dans les petits espaces restants, et ainsi de suite :
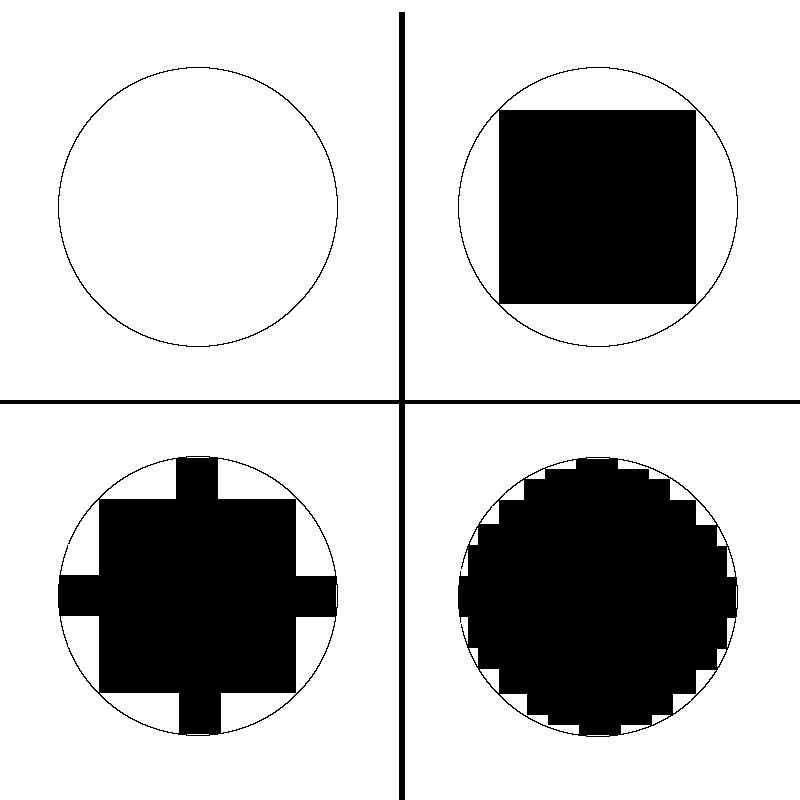
Dans un monde où l’on ne peut parler qu’en termes de carrés, cette façon de procéder permet de reconstituer un cercle petit à petit, mais aussi un triangle, un octogone, etc.
Il suffit juste, pour chaque carré placé, de savoir ses dimensions et où le placer. C’est tout. On n’a plus besoin de savoir découper une faïence en cercle, par exemple.
On note déjà que plus on utilise de petits carrés, plus on s’approche du cercle. On a donc un compromis à faire : réduire le nombre de carrés pour gagner du temps (mais perdre en fidélité), ou mettre plus de carrés et gagner en fidélité (quitte à devoir y passer beaucoup plus de temps).
Application au traitement du signal
Dans le cas du traitement du signal, on n’approche plus des cercles avec un ensemble de carrés, mais on approche un signal compliqué avec une somme de signaux sinusoïdaux simples.
En effet, la sinusoïde est le signal le plus simple à produire à partir d’un alternateur (le système le plus courant pour produire de l’électricité). Les fonctions telles que le sinus sont intimement liés à tout mouvement rotatoire (de l’alternateur).
Préambule sur la somme des fonctions
Ce qu’il faut voir avec des fonctions mathématiques, c’est qu’on peut les additionner pour obtenir une nouvelle fonction. Si l’on se représente les fonctions par une courbe, alors la somme de deux fonctions en un point donné est égale à la somme de valeurs de cette fonction en ce point.
Par exemple, la somme des fonctions sinus et cosinus au point $\frac{\pi}{4}$ est $sin(\frac{\pi}{4}) + cos(\frac{\pi}{4})$, soit $\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}$ soit $\sqrt{2}$. En faisant la même chose pour tous les points de la courbe $sin(x)$ et $cos(x)$, on obtient la courbe de la fonction correspondant à $sin(x)+cos(x)$.
Ceci est peut-être trivial pour vous, mais je sais que ça ne l’est pas pour tout le monde, et donc je préfère le mettre ici : on peut additionner des fonctions, et ça revient à additionner les points des fonctions entre eux.
Application à la série de Fourrier
La série de Fourrier consiste en une somme de plein de fonctions, autant que l’on souhaite, en fait.
Pour l’explication, allons-y doucement.
Imaginons que l’on ait envie d’obtenir un signal de type « carré », ou « créneaux ». D’après le théorème de Fourrier, ce signal, comme tous les autres, peut être reconstitué à partir d’une somme de sinusoïdes.
Pour « imiter » le signal carré, on peut commencer par utiliser un sinus simple de la même fréquence de base que le signal carré :

Ci-dessus, on voit un sinus simple avec la même fréquence que le créneau que l’on souhaite. La fréquence étant la même, on dit que cette sinusoïde est la fondamentale. Les deux courbes se ressemblent, mais on peut évidemment faire beaucoup mieux.
Par exemple, on voit qu’au niveau des crêtes, la sinusoïde dépasse le créneau. Inversement, au niveau des « coins » du créneau, la sinusoïde est plus basse.
Dans l’ensemble, il faut ajouter au sinus de base un autre sinus qui viennent s’additionner dans les coins et se soustraire au niveau des crêtes. Là où la sinusoïde et le créneau se croisent, il n’y a idéalement rien à ajouter ou à retirer.
Ci-dessous, je vous propose une telle sinusoïde, qui est positive, négative, et nulle aux endroits décrits ci-dessus :

Maintenant, si l’on additionne la sinusoïde fondamentale avec la nouvelle, on obtient une nouvelle fonction, qui n’est pas encore le signal carré mais qui s’en approche un peu plus que la sinusoïde seule :
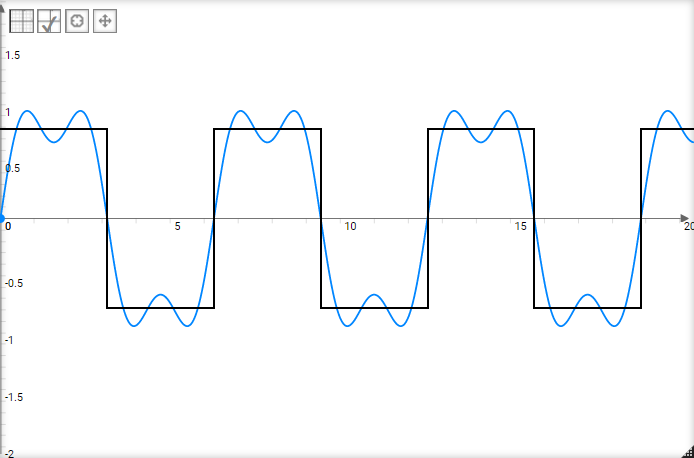
On peut répéter l’opération plusieurs fois : en cherchant à chaque fois une fonction qui soit positive ou négative aux bons endroits. En l’occurrence, pour notre prochaine étape, on ajoute la fonction ci-dessous :

Ce qui donne, quand on l’ajoute à la courbe bleue :
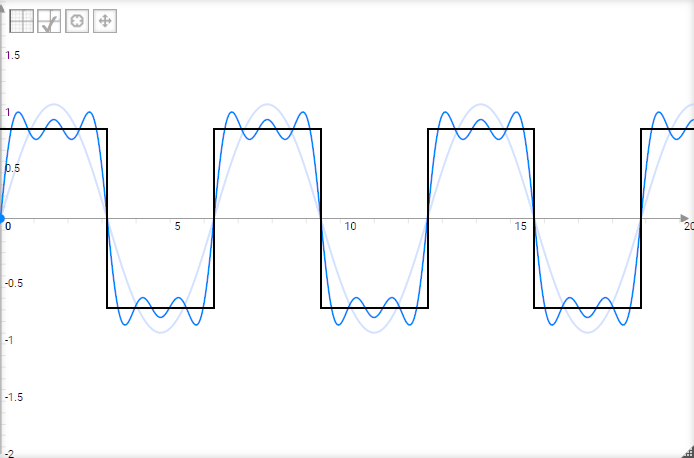
En fait, pour obtenir un signal carré de fréquence $f$, on ajoute entre elles toutes les harmoniques impaires du signal fondamental, donc de fréquence 3, 5, 7… fois la fondamentale ; et à chaque fois d’une amplitude de plus en plus petite d’un rapport 1/3, 1/5, 1/7… car il s’agit simplement de faire des ajustements de plus en plus fins.
Quand on a fait l’opération 5, 10, 50 fois, on s’approche de plus en plus du signal carré :

Idéalement, il faudrait faire une somme infinie, là on aurait un vrai signal carré.
Évidemment, envoyer une liste infinie de sinus à additionner est contre-productif (et impossible) : on cherche avant tout à réduire la quantité de données à transmettre, pas à l’étendre à l’infini !
On choisit donc généralement de n’envoyer qu’un certain nombre de sinusoïdes. Le choix dépendant alors de la fidélité que l’on souhaite obtenir et de l’espace de stockage numérique dont on dispose. On parle aussi du choix du niveau de compression.
Cette méthode où un ensemble de signaux sinusoïdaux — le signal le plus fondamental que l’on peut produire — permettent d’approcher un signal différent — ici le signal carré — constitue le principe de base des séries de Fourrier.
Le signal carré (ou créneau) est difficile à obtenir avec de l’électronique, mais il reste cependant une fonction « basique » en traitement du signal. Parmi les autres signaux « basiques », citons le signal triangulaire et signal en dents de scie.
Dans les trois cas, on peut approcher ces signaux en commençant par une sinusoïde de la fréquence de base, puis en ajoutant différentes harmoniques :
- Pour le signal carré, je l’ai mentionné, on ajoute les harmoniques impaires ;
- Pour le signal en dents de scie, on ajoute toutes les harmoniques paires et on retranche toutes les harmoniques impaires ;
- Pour le signal triangulaire, on ne considère que les harmoniques impaires, et l’on en alterne les signes devant ces harmoniques impaires.
Ces signaux basiques restent simples. Mais on peut appliquer le même principe à tous les signaux. Par exemple une chanson. Et ça, c’est exactement ce que fait le format MP3.
Application au MP3
En enregistrant un signal sonore au format MPEG-Layer Audio 3, ou MP3, on procède à une analyse méticuleuse de l’enregistrement sonore brut : on va en sortir toutes les fréquences qu’on y décèle. On fait donc l’inverse de ce qu’on a fait ci-dessus, mais on le fait informatiquement, pas en tâtonnant à la main. C’est sous la forme d’une liste de fréquences sinusoïdales que l’encodeur MP3 va enregistrer un fichier « .mp3 ». C’est tout.
Pour le MP3, il se pose la question de la qualité audio, et c’est d’ailleurs la première chose qui se fait. L’enregistrement sonore brut est constitué de milliers de points de mesure du son, chaque seconde (un peu comme une image est un ensemble de milliers de pixels, et que l’on diminue le nombre de pixels pour réduire le fichier).
Si l’on veut que notre fichier pèse moins lourd, on supprime des points, par exemple la moitié des points. Forcément on perdra de l’information, mais l’enregistrement restera audible.
En fait, quand on a un MP3 en 320 kbps, on a un enregistrement où chaque seconde de musique contient 320 000 enregistrements sonores. Si l’on a un fichier en 128 kbps, alors on n’en a plus que 128 000. C’est pour cela que le fichier en 128k est plus léger qu’un 320k, mais c’est aussi la raison pour laquelle sa qualité est plus médiocre.
Ce n’est qu’une fois que l’on a supprimé des points de données que l’on procède à son analyse de Fourrier. Bien sûr, plus on a éliminé de points, plus l’analyse est rapide. Si vous avez déjà encodé des fichiers MP3, vous avez dû le constater.
Par ailleurs, une fois que les différentes fréquences sont listées, on peut compresser davantage. En effet, certaines fréquences sont inaudibles par l’oreille humaine. D’autres sont par exemple inutiles pour certaines applications. Les hautes fréquences et les basses fréquences sont inutiles pour téléphoner, par exemple : c’est pour ça que pour les appels téléphoniques on ne conservait que les fréquences entre 300 Hz et 3 400 Hz. C’était suffisant pour se comprendre, même si le son semblait mauvais.
Le MP3 n’est ici donné qu’à titre d’application moderne et courante de la vie de tous les jours de l’outil de la décomposition en séries de Fourrier. Il y a beaucoup d’autres applications, notamment là où un grand nombre de signaux périodiques s’entremêlent.
Par exemple, la prédiction des marées : une marée doit être prédite pour des raisons pratiques dans le monde maritime, mais ce phénomène est complexe et fait intervenir la rotation terrestre, la révolution de la Lune autour de la Terre ainsi que celle de la Terre autour du Soleil, et d’autres paramètres.
Heureusement, tous ces phénomènes cosmiques sont sensiblement périodiques : à l’aide de la décomposition de Fourrier, on peut fabriquer des modèles qui analysent tout ça et permettent de produire une fonction complexe qui donnent les horaires des marées ainsi que leur coefficient avec une fiabilité remarquable.
Conclusion
L’analyse de Fourrier permet de décomposer mathématiquement un système ondulatoire compliqué en une somme de signaux très simples.
Comme très souvent, donc, on décompose un problème compliqué en plusieurs problèmes simples (et solubles).
C’est une branche mathématique utilisée partout en physique, mais aussi comme on l’a vu, en informatique, y compris dans la vie de tous les jours.
Pour info, comme souvent, avant les ordinateurs et les calculateurs électroniques, il existait des machines entièrement mécaniques pour faire les analyses harmoniques à partir des séries de Fourrier, et c’est assez spectaculaire à voir en œuvre. Une machine remarquablement similaire existe pour prédire les marées (et a été mise au point par Kelvin).
Enfin, une dernière chose : les séries de Fourrier ne sont pas à confondre avec la transformée de Fourrier, qui est aussi un outil mathématique, mais encore autre chose (même si on y retrouve une idée similaire de décomposition des signaux compliqués en systèmes plus simples).