
Les fonctions trigonométriques sont apprises dès le collège : cosinus, sinus et tangente respectivement notées $cos(x)$, $sin(x)$ et $tan(x)$.
À l’école ce sont juste des fonctions un peu marrantes qui ressemblent à des vagues :

Mais savez-vous d’où viennent ces fonctions ?
Le cercle de rayon 1
Pour savoir d’où viennent les fonctions trigonométriques on va devoir dessiner un cercle de rayon 1 :
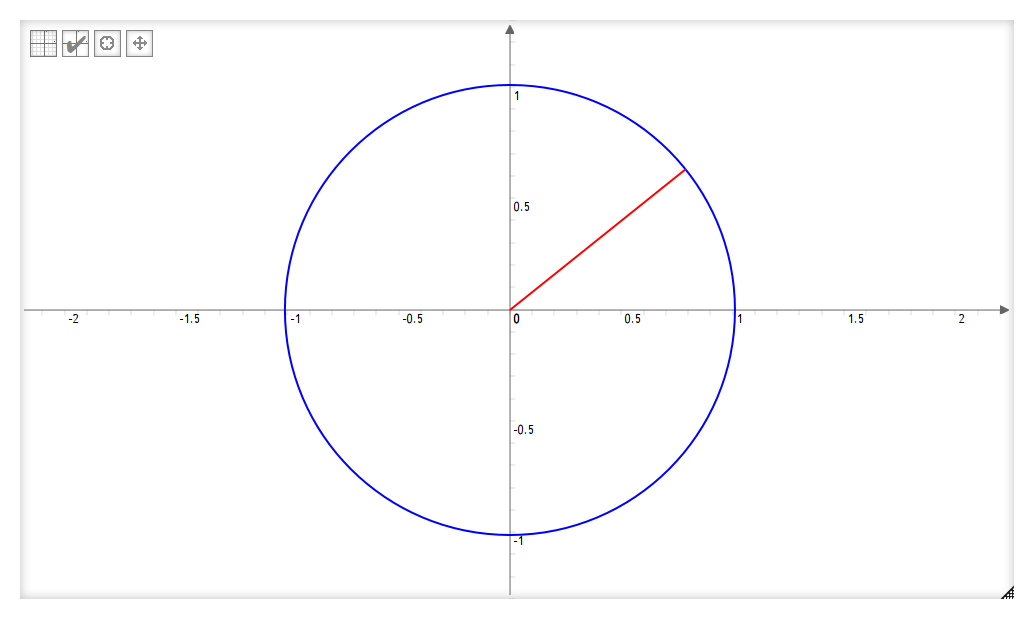
En rouge j’ai placé son rayon.
Maintenant une question : quelle est la valeur de l’angle formé par le rayon rouge et l’axe horizontal ? Vous n’avez droit qu’à une règle, pas de rapporteur d’angles.
La solution consiste à mesurer les longueurs des projections du rayon sur l’axe des abscisses et des ordonnées :
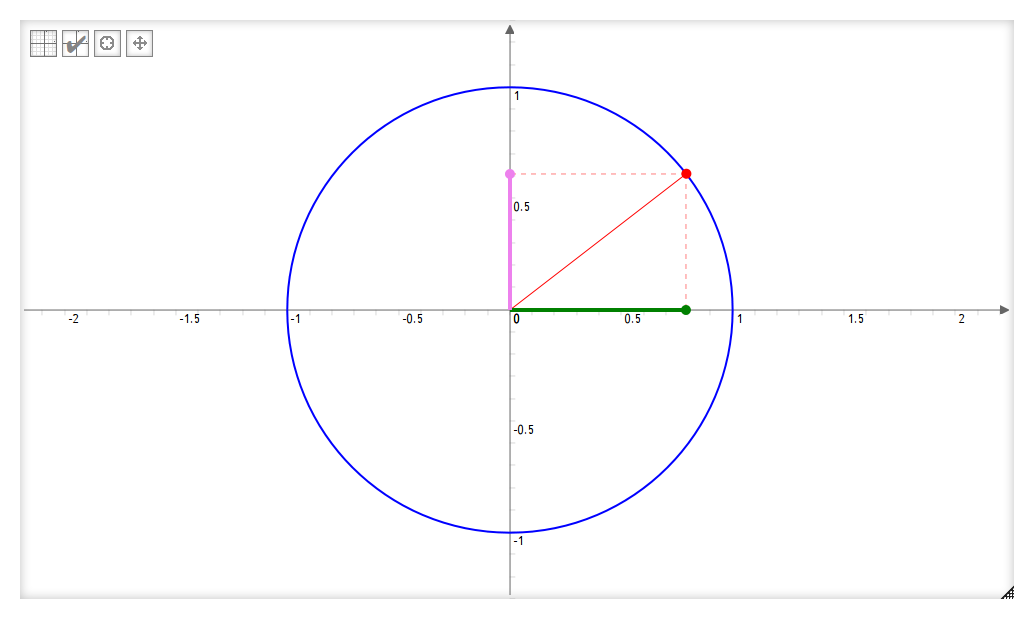
On obtient deux segments, ici en violet et en vert.
Sinus et Cosinus
Sur l’image précédente, les deux segments portent un nom : celui en violet correspond au sinus. Ce terme provient du nom d’un des deux petits côtés d’un triangle rectangle : le grand côté est appelé hypoténuse, et les deux petits sont appelés sinus et co-sinus (cosinus).
Dans le cercle trigonométrique, fortement lié au triangle rectangle (comme on va le voir plus bas), on note que le sinus est le côté vertical et est son homologue horizontal, sur l’axe des abscisses, est le cosinus.
Vous imaginez que si l’angle change, alors les sinus et cosinus vont également changer.
En fait, à chaque angle entre 0° et 360° correspond un couple de nombres [sinus, cosinus] unique.
Sur cet exemple, on mesure à la règle :
- sinus : 0,61
- cosinus : 0,77
Or, l’angle qui correspond à ça est un angle de 37,6 degrés.
Le sinus et le cosinus permettent donc de calculer un angle simplement avec une règle graduée. À l’inverse, à partir d’un angle, on peut aussi calculer les valeurs de son sinus et son cosinus.
Ces deux nombres ne sont pas les seuls que l’on trouve dans un cercle unitaire, loin de là !
Tangente et Cotangente
Je suis sûr que tout le monde connait la tangente (notée $tan(x)$). Par contre, la cotangente (cotée $cot(x)$ ou $cotan(x)$) est moins connue. Ces nombres vont également de pair.
Ils ne se trouvent plus dans le cercle mais à l’extérieur du cercle :
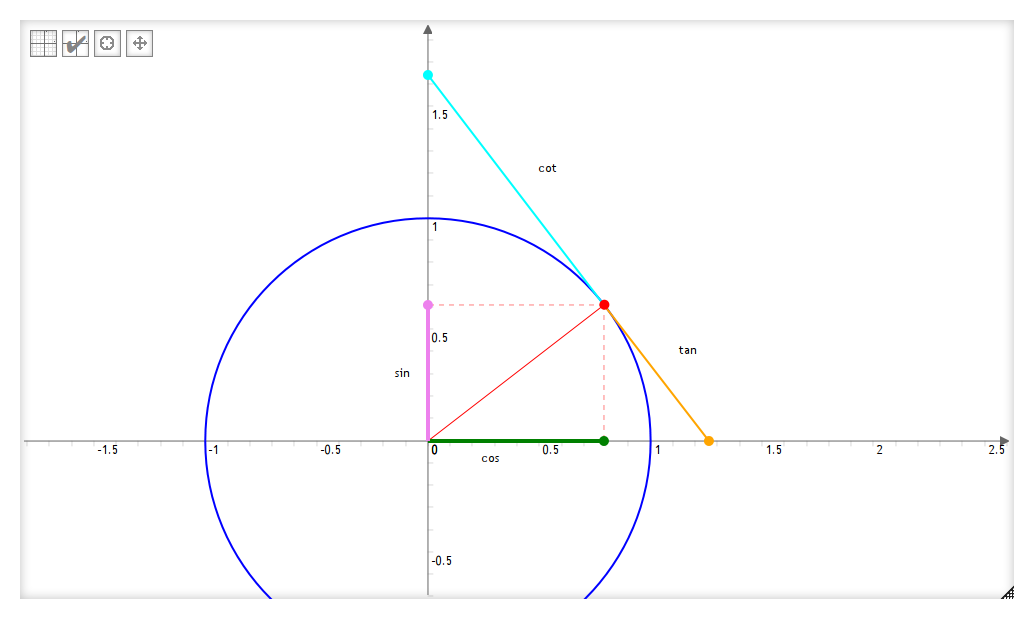
Sécante et Cosécante
Beaucoup moins connues : la sécante (notée $sec(x)$) et la cosécante (notée $csc(x)$). Idem, ces nombres vont là aussi de pair. Ce sont un peu les équivalents de sinus et cosinus, mais se prolongent à l’extérieur du cercle jusqu’à l’intersection avec la tangente :

Les autres fonctions
En plus de sinus, tangente, sécante, cosinus, cotangente et cosécante il y a d’autres fonctions.
On trouve ainsi :
Les fonctions « verse » :
- le sinus verse (noté $versin(x)$), qui est dans le cercle à côté du cosinus et qui représente la partie manquante au cosinus pour arriver au rayon 1.
- le cosinus verse (noté $cvs(x)$), qui est similaire au sinus verse, mais sur l’axe des ordonnées).
Les fonctions « ex » :
- l’exsecante (notée $exsec(x)$), qui correspond à la partie de la sécante qui est à l’extérieur du cercle ;
- l’excosécante (notée $excsc(x)$), qui est la même chose mais pour la cosécante.
Si on représente tout ça, on obtient ceci :
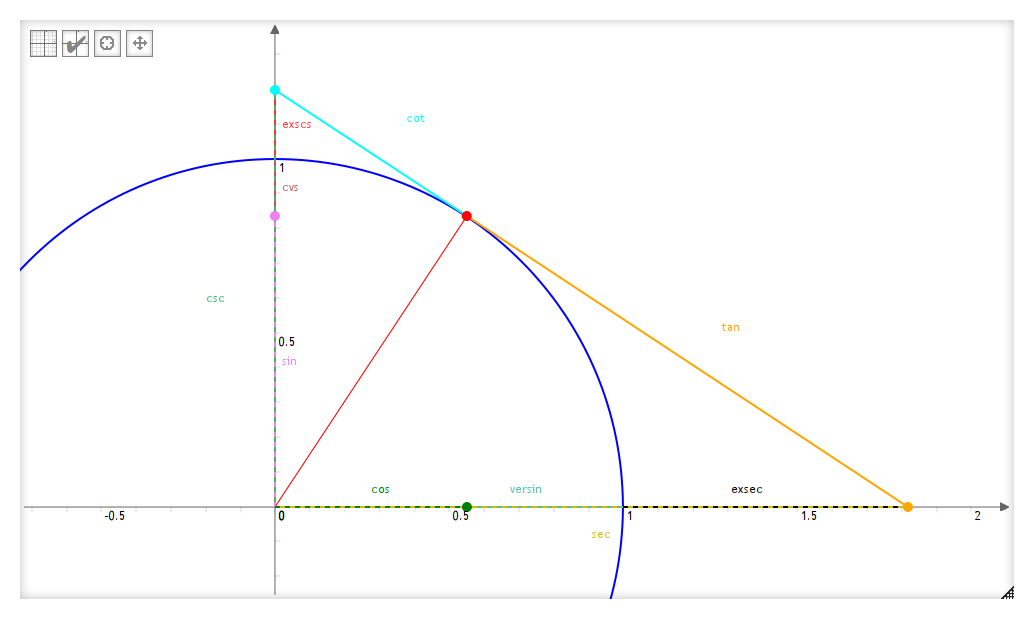
Vous pouvez vous amuser avec toutes ces fonctions dans cet outil que je vous ai fait : Les fonctions Trigonométriques.
Relations entre toutes ces fonctions
Toutes ces fonctions sont liées. En dépendent toutes du cercle unitaire et de l’angle que l’on place dedans.
Je ne vais pas tout détailler : certaines relations sont simples à deviner, par exemple on voit tout de suite que l’on a :
- $cos(x) + versin(x) = 1$
- $cos(x) + versin(x) + exsec(x) = sec(x)$
Ces relations sont présentes mais ne servent pas à grand-chose.
Il y a une relation, en revanche, qui est très connue et plus utile : $cos^2(x) + sin^2(x) = 1$.
D’où vient cette relation ? En fait, c’est très simple à voir : c’est le théorème de Pythagore appliqué au cercle unitaire sur le triangle formé par le rayon et les axes du graphique :

Par projection, l’angle en bas est un angle droit et on applique alors le théorème de Pythagore, d’où la relation.
Ceci est également la raison pour laquelle on retrouve la trigonométrie dans les triangles : implicitement, le triangle possède divers cercles qui lui sont associés (cercle circonscrit, cercle inscrit…) et auxquels on peut appliquer la trigonométrie.
« trigonométrie » vient d’ailleurs du grec avec « tri » (trois) et « gono » (angle) : la trigonométrie est donc également très liée aux triangles, en plus des cercles.
Les fonctions « inverse »
La fonction sinus appliquée à un angle donne le sinus de cet angle. Ainsi on a par exemple $sin(30^{\circ}) = \frac{1}{2}$.
La fonction inverse du sinus est la fonction qui donne un angle à partir du sinus. Cette fonction se nomme arcsinus (notée $arcsin(x)$ ou $asin(x)$, ou même parfois $sin^{-1}(x)$).
On a donc $arcsin(\frac{1}{2}) = 30^{\circ}$.
De même, il existe les fonctions arccosinus et arctangente.
Les Radians
Le nom de la fonction arcsinus vient du fait qu’à partir du sinus on obtient un arc (en rouge) sur le cercle trigonométrique :
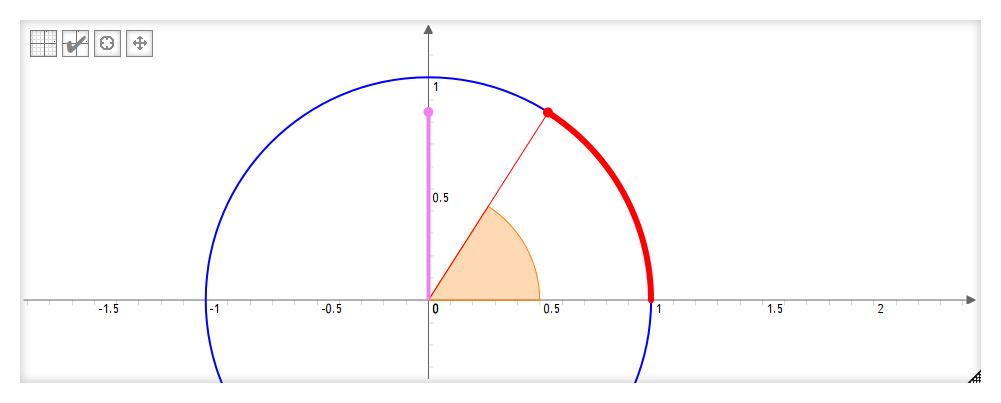
Cet arc est une portion du périmètre du cercle, dont la longueur dépend directement de l’angle.
Si l’angle fait 60°, et vu que le tour complet du cercle faire 360°, alors l’angle fait 1/6 du cercle. L’arc de cercle mesure donc 1/6 du périmètre, soit 1/6 de $2\pi$. Or, 1/6 de $2\pi$, ça fait aussi $\frac{\pi}{3}$.
On remarque que l’on peut donc mesurer un angle en utilisant la portion du périmètre qu’il représente sur un cercle unitaire. Cette unité d’angle est appelée le radian.
Le périmètre du cercle complet étant $2\pi$, un angle de $2\pi \text{ rad}$ correspond à 360°.
De même, $\pi \text{ rad}$ correspond donc à 180° (la moitié de $2\pi \text{ rad}$). Un angle de 90°, c’est alors $\frac{\pi}{2} \text{ rad}$, et ainsi de suite.
En général, on ne calcule pas la valeur numérique des radiants ($2\pi$ vaut environ 6,28). On conserve la notation exacte avec $\pi$. C’est pour ça qu’on trouve souvent $\pi$ dans les angles ou associés aux fonctions trigonométriques ($sin(\pi)$, par exemple).
Le radian, contrairement aux degrés et aux autres unités d’angles, est l’unité légale de mesure des angles.
La trigonométrie hyperbolique
Pour expliquer l’origine des fonctions trigonométriques, je suis parti d’un cercle de rayon 1 (un cercle unitaire). C’est normal : c’est de là que viennent les fonctions trigonométriques circulaires (sinus, cosinus…).
On peut partir d’une autre forme géométrique. Si on part d’une hyperbole, on obtient la trigonométrie hyperbolique :

Le principe est le même que pour le cercle : il suffit de prendre un point sur la courbe et son ordonnée correspond à son sinus hyperbolique (noté $sinh(x)$) et son abscisse correspond à son cosinus hyperbolique (noté $cosh(x)$). Les autres fonctions (tangente, etc.) existent là aussi, et les fonctions inverses également (argument sinus hyperbolique (noté $argsinh(x)$) et argument cosinus hyperbolique (noté $argcosh(x)$)).
À quoi tout ça sert-il ?
Les fonctions trigonométriques de base (sinus, cosinus, tangente) sont très utilisées un peu partout, y compris en physique.
Le sinus, par exemple, représente la hauteur (par rapport au centre) d’un point situé sur un cercle. Si ce cercle tourne, alors le point tournera avec lui, comme sur cette animation : si on fait défiler le cercle trigonométrique, on voit apparaître les courbes « en vague » du sinus et du cosinus.
Or, des systèmes rotatifs, il y en a partout : les pales d’une hélice, les roues d’une voiture ou d’un vélo, l’axe d’un moteur, l’aimant dans une dynamo, la Terre qui tourne sur elle-même, la Terre qui tourne autour du Soleil…
De plus, les fonctions trigonométriques ressemblent à des vagues : les ondes et les vagues obéissent également à des fonctions sinusoïdales : ondes sonores, ondes électromagnétiques, etc.
Les fonctions trigonométriques se retrouvent donc un peu dans tous les domaines de la physique et de la science en général.
Comme les dérivées, donc, la trigonométrie non plus n’est pas juste un délire de matheux : elle a une origine géométrique basée sur un cercle (ou une hyperbole, dans le cas de la trigonométrie hyperbolique), et se retrouve donc dans tous les systèmes impliquant des cercles, des roues, des sphères en rotation.