
L’effet tunnel est un exemple d’effet étrange mentionné dès que l’on parle de physique quantique. À quoi correspond-il ? Comment l’expliquer ?
La définition de l’effet tunnel, si je prends Wikipédia, c’est ça :
L’effet tunnel désigne la propriété que possède un objet quantique de franchir une barrière de potentiel même si son énergie est inférieure à l’énergie minimale requise pour franchir cette barrière.
Ça semble très compliqué, et cet article va essayer de clarifier tout ça.
Dans cette définition, ce qu’ils appellent « un objet quantique » est typiquement une particule élémentaire, par exemple un électron. Dans la suite de l’article, l’on prendra effectivement un électron en exemple, mais le principe reste similaire pour toute autre particule.
Modèle atomique
On dépeint classiquement un atome comme des électrons sur des orbites fixes autour d’un noyau central. Cette vision est populaire, mais loin de la description moderne de l’atome. Comme expliqué dans mon article sur le modèle atomique et les couches électroniques, on sait aujourd’hui que les orbites des électrons ne sont pas comme ça. En fait, même les électrons ne sont pas comme ça : on ne les voit plus comme des petites billes.
Dans la compréhension moderne du modèle atomique, les électrons sont représentés par une fonction d’onde ayant une composante probabiliste. Cela veut dire que l’électron correspond à tout le nuage à la fois. Le nuage contient l’électron et ce dernier ne prend une position fixe que lorsqu’on le mesure. Cette position enfin, est, elle, définie par des probabilités.
L’on connait très bien les probabilités, mais pas l’issue de ces probabilités. Voyez ça comme un jeté de dés : on sait que l’on a très exactement une chance sur six de faire un 6, mais on ne sait pas prévoir si le prochain lancé sera effectivement un 6.
Cette nuance est très importante et elle a deux conséquences :
- La première c’est que ce n’est pas parce que l’on a à faire à des probabilités que l’on nage dans le flou. On connait les probabilités.
- Inversement, la parfaite connaissance de règles de probabilité ne nous donne pas une vue sur l’avenir pour autant. Les probabilités sont connues, pas leur issue.
Poursuivons. Un nuage — météorologique je veux dire — n’est pas clairement délimité. De loin, on voit une zone aux allures finies, mais quand on s’en approche, on entre dedans de façon très progressive, comme dans un brouillard. Si l’on voulait délimiter ce nuage, il faudrait poser une règle arbitraire. Par exemple « le moment où l’air contient 25 gouttelettes par mètre cube, pas avant », ou encore « le moment où 5 % de la vision est obstruée par des gouttelettes ».
En physique quantique, c’est un peu pareil. Le nuage électronique autour d’un atome s’étend théoriquement jusqu’à l’infini, et englobe donc tout l’univers. Pour que l’on puisse avoir une représentation plus compréhensible, on va délimiter la zone qui a une probabilité de 90 % de trouver l’électron. Dans ce cas, l’électron a 90 % de chance de se trouver dans cette limite et seulement 10 % ailleurs ; où « ailleurs » est synonyme de « partout ailleurs dans l’univers » :

Cette probabilité peut être représentée par une fonction : la fonction de distribution de présence de l’électron. En particulier, la fonction de distribution radiale donne la probabilité de présence en fonction de la distance au noyau, le tout dans une direction donnée — les nuages électroniques n’étant pas forcément isotropes, on aura aussi une composante directionnelle, ou angulaire, autour du noyau, mais on va ignorer ça pour le moment (et de toute façon elles n’ont pas d’importance pour les électrons 1s ou 2s).
La représentation graphique en 2D de la fonction de distribution radiale donne une courbe, où l’origine représente le centre du noyau, x la distance à ce noyau et y la probabilité de trouver l’électron.
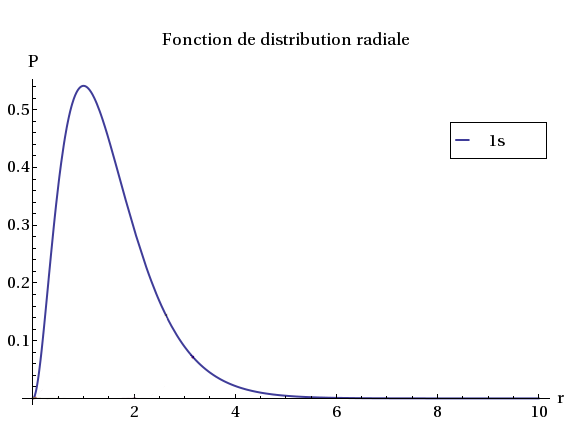
Pour l’orbitale 1s de l’hydrogène ci-dessus, il y a un seul lobe qui est une sphère centrée sur le noyau. La probabilité est nulle au niveau du centre du noyau lui-même, élevée au niveau du rayon atomique (r=1), mais décroît ensuite très vite vers zéro si l’on s’en éloigne.
La probabilité de trouver l’électron 1s loin du noyau est donc très faible. Faible, mais pas nulle.
Notion de barrière de potentiel
Une barrière de potentiel, classiquement, c’est une colline vers laquelle l’on fait rouler un ballon. Si le ballon ne va pas assez vite, alors elle ne franchira pas la colline. Le potentiel gravitationnel est trop élevé pour que le ballon, qui n’a pas suffisamment d’énergie, puisse le vaincre.
En soi, un potentiel peut être de n’importe quelle nature : potentiel électrique, chimique, magnétique, gravitationnel… Si l’on fait rouler un aimant vers un champ magnétique, il peut être repoussé également, faute de rouler assez vite.
Pour l’électron d’un atome donné, la barrière de potentiel peut-être un champ électrique porté par un autre atome. Toutefois, contrairement au ballon qui est totalement stoppé par la colline et ne passera donc jamais la barrière s’il n’a pas assez de vitesse, l’électron n’est pas totalement stoppé lorsqu’il rencontre le second atome : sa probabilité de présence dans l’autre atome est simplement atténuée.
Ainsi, au lieu d’une fonction de distribution comme celle plus haut qui serait tronquée à cause de la barrière, on peut avoir une courbe où la barrière ne fait qu’atténuer la fonction, sans la bloquer complètement :
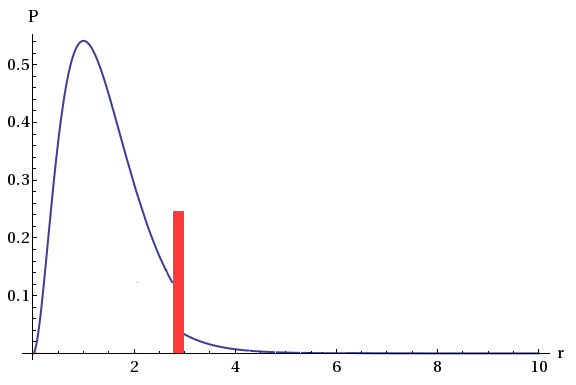
(cette représentation est faite habituellement avec la fonction d’onde directement, pas avec la fonction de distribution, mais les deux sont liées et cette représentation me semble plus simple à comprendre)
Ce qu’il faut voir ici, c’est que si l’on mesure la position de l’électron, alors elle sera de l’autre côté de la barrière seulement 1 % du temps, alors que sans la barrière on aurait pu avoir 10 %. La probabilité d’avoir l’électron de l’autre côté de la barrière est clairement diminuée, mais pas annulée, elle peut s’y trouver, quand bien même cette barrière était initialement trop élevée par rapport à l’énergie de l’électron.
Maintenant, l’on peut imaginer de l’autre côté un atome qui va « emprisonner » notre électron à l’instant même où il aura franchi la barrière. Il suffira donc juste que l’électron se présente de l’autre côté pour l’y piéger. Piéger l’électron revient à modifier sa probabilité de présence afin que désormais, elle soit 99 % à droite et seulement 1 % à gauche. En somme : on l’empêche de retourner d’où elle vient.
Ce piège peut être réalisé par la présence d’un autre atome en manque d’électron (un ion, un cation). D’un point de vue classique : l’électron est alors comme capté par ce cation après s’être échappé de son atome initial. Dans ce cas, on parle d’un puits de potentiel. Classiquement, c’est comme si le ballon tombait dans un trou et y restait.
Si l’on fait le bilan : on a donc un électron qui est passé de l’autre côté d’une barrière alors qu’il n’avait pas l’énergie pour ça initialement. Aucun effet classique ne peut l’expliquer : seule la physique quantique le peut. Cet effet est réel, et c’est cela que l’on appelle l’effet tunnel.
La dénomination provient du fait que si l’on appliquait ça à un ballon, le ballon devrait creuser un tunnel à travers la barrière, à défaut de passer par-dessus.
Comment c’est possible ?
Nous n’avons pas d’yeux suffisamment petits pour aller voir directement le mécanisme responsable de l’effet tunnel. Cela n’empêche pas de voir l’effet ou ses conséquences se produire.
La seule façon de se représenter ça, c’est mathématiquement, avec des équations. L’expérience est alors là pour comparer la réalité à nos prédictions mathématiques, et une concordance permet alors de dire si notre modèle théorique fonctionne ou non. Et la physique quantique, pour le moment, fonctionne incroyablement bien. Les sciences physiques c’est ça : retrouver par l’expérience, par des essais successifs, le modèle mathématique qui décrit le mieux un phénomène rencontré, puis de valider cette équation.
Une équation ne donne pas la raison de l’existence du phénomène, mais elle nous dit si le phénomène s’applique, et si oui, dans quelle mesure. La raison de son existence est une autre question à laquelle répondre est parfois plus délicate.
Pour dire pourquoi et comment ça marche, toutefois, il faut voir que l’électron, son paquet d’onde en fait — l’objet qui combine la particule et l’onde — va interagir avec la barrière de potentiel (ou l’objet qui lui donne source).
Cette interaction est telle que plus le paquet d’onde pénètre dans la barrière, plus elle est atténuée. Et plus il s’atténue, plus il sera enclin à plutôt rebondir contre la barrière :
Si la barrière de potentiel est fine, alors elle n’est pas totalement atténuée lorsqu’elle atteint l’autre côté de la barrière : elle peut donc en ressortir avec une probabilité décente et observable.
Dans la vie courante, on peut observer un phénomène analogue à une impulsion sonore. Quand un son rencontre un obstacle, il y a toujours une partie de l’onde qui est réfléchie, et une partie qui est transmise dans l’obstacle. Si l’obstacle est épais, l’onde transmise finira dissipée et ne sera pas audible de l’autre côté. Si l’obstacle est très fin, la partie transmise franchira l’obstacle en passant à travers.
Ainsi, si l’on est dans une cathédrale, les murs en pierre épais vont favoriser une réflexion des ondes sonores : c’est ce qui donne cet effet de résonance et d’écho. Si l’on recouvrait tous les murs de mousse isolante, l’écho disparaît : l’onde est absorbée et dissipée en chaleur, plutôt que réfléchi ou transmise. Et si l’on remplaçait les murs par des fines cloisons en papier, l’onde sonore va mettre en vibration le papier et quelqu’un de l’autre côté vous entendra facilement : l’onde est transmise sans être ni absorbée ni réfléchie.
Pour un paquet d’onde, on veut le voir de façon similaire : le paquet d’onde va en partie rebondir sur la barrière de potentiel, et en partie pénétrer à l’intérieur, voire, si la barrière est fine, passer à travers.
En n’oubliant pas — et c’est là où l’analogie avec l’onde sonore s’arrête — que le paquet d’onde ne passe pas partiellement à travers : elle n’est pas divisée en deux. C’est sa probabilité qui l’est. Mais l’électron lui-même n’est pas sécable et sa présence ne se mesure toujours qu’à un endroit : on pourra observer la particule aussi bien dans l’un que dans l’autre, par exemple en répétant l’expérience plusieurs fois de suite avec plusieurs électrons : une partie des électrons seront réfléchis par la barrière de potentiel, et une autre partie auront réussi à traverser la barrière de potentiel.
Où observer ce phénomène ?
On voit les conséquences de l’effet tunnel tous les jours et on sait même le mettre à profit.
Dans la nature, un exemple notoire est qu’il fait briller le Soleil. L’énergie nucléaire des étoiles provient de la fusion des protons. Les protons fusionnent quand leur énergie cinétique leur permet de dépasser leur répulsion électrique. Cette répulsion constitue une barrière, appelée barrière Coulombienne, et qui est un type de barrière de potentiel.
Au cœur du Soleil et de beaucoup d’étoiles, la température est trop faible pour que la seule énergie cinétique des protons permette aux particules de franchir la barrière coulombienne. Il faudrait en effet des températures de l’ordre de 100 millions de kelvins, mais le Soleil n’est toujours qu’à 15 millions de kelvins.
Pourtant, la fusion se produit bien. Une explication réside avec l’effet tunnel : on explique le franchissement de la barrière coulombienne par l’effet tunnel. Une fois de l’autre côté de la barrière, les deux protons sont maintenus ensemble par l’interaction forte, qui constitue un puits de potentiel. La température thermodynamique rapproche les protons, mais l’effet tunnel est nécessaire pour ce dernier coup de pouce permettant d’obtenir la fusion.
Quant à l’exploitation artificielle de l’effet tunnel dans notre technologie, on peut citer : la mémoire flash des clés USB, cartes SD, mémoires de téléphones, disques SSD. Ils fonctionnent en piégeant des électrons sur des conducteurs isolés électriquement (les grilles flottantes — ou floating gate). L’isolant est franchi par effet tunnel, et les charges électriques ainsi chargées ou déchargées sur des pastilles isolantes constituent alors les bits stockés dans la mémoire.
Une autre application bien connue est le microscope à effet tunnel : on mesure un courant d’électron plus ou moins fort (permettant de faire des pixels plus ou moins lumineux d’une image globale), et ces électrons passent de l’échantillon au détecteur par effet tunnel.