
Cet article fait partie d’une série d’articles à l’occasion de la 26e CGPM (en 2018), à l’occasion de laquelle le kilogramme va être redéfini de façon historique :
- Comment le kilogramme va être redéfini (le présent article)
- Pourquoi redéfinir le kilogramme ?
Jusqu'en 2018, sur les 7 unités de base du système international, le kilogramme était la seule à être définie à partir d’un objet matériel : un étalon en alliage de platine et d’iridium conservé à côté de Paris et qui servait de référence du kilogramme au monde entier.
Cela faisait plus d’un siècle que cet objet représente le kilogramme, et non sans poser quelques problèmes lié au temps : l’usure, l’unicité et le fait qu’il soit conservé en France et pas ailleurs constituent des problèmes d’ordre technique, pratique et politique.
J. C. Maxwell (1831 - 1879, physicien connu entre autres pour les équations de Maxwell en électromagnétisme) écrira :
« Même si le repère cylindrique du kilogramme est abrité dans un coffre spécial, dans des conditions contrôlées au BIPM, sa masse (théorique) peut dériver légèrement au fil des ans et il est sujet à des modifications de masse (théorique) en raison de la contamination, la perte de matériau de surface par nettoyage, ou d'autres effets. Une propriété de la nature est, par définition, toujours la même et peut en théorie être mesurée n'importe où, alors que le kilogramme au BIPM pourrait être endommagé ou détruit. »
À l’image du mètre, qui n’est plus défini à partir d’un morceau de métal mais à partir de la vitesse de la lumière, les métrologues cherchaient depuis longtemps comment redéfinir le kilogramme pour ne plus avoir à dépendre d’un objet physique si fragile. Et il ont fini par trouver.
En 2018, le kilogramme est devenu, enfin, une unité dépendante seulement d’une constante physique intrinsèque de la nature.
Voyons ici la méthode qui fut retenue. Vous allez voir, elle est astucieuse et ingénieuse, mais également très technique !
La nouvelle définition du kilogramme
Pour résumer rapidement, on a utilisé le kilogramme « K » pour mesurer la constante de Planck (une constante utilisée en physique quantique), puis fixé la valeur de cette dernière, puis défini le kilogramme en fonction de la constante de Planck.
Cela peut sembler un serpent qui se mort la queue, mais ça ne l’est pas. En réalité, c’est plutôt un changement de référence.
Plutôt que d’avoir un kilogramme à partir de laquelle on mesurait la constante de Planck, on va chercher à fixer la constante à une valeur qui restera dès lors immuable, et à partir de laquelle on redéfinira ce qu’on désigne par « le kilogramme ».
Ainsi, le kilogramme étalon en platine ne nous est plus d’aucune utilité.
Si l’on désire retrouver la masse d’un kilogramme, il suffit de prendre la constante de Planck et un balance de Kibble et de mesurer la masse d’un kilogramme.
Quant à la constante de Planck… C’est maintenant elle qui est la référence : on n’a plus besoin de la mesurer.
Et comme elle est une constante fondamentale de la nature, elle ne changera pas : elle ne peut pas s’user, se détériorer ou se perdre.
Ci après, le fonctionnement de la balance de Kibble.
La balance de Kibble (ou balance de Watt)
Une balance de Kibble (ou anciennement la balance de Watt), comme toutes les balances permet de comparer deux forces. Pour une balances classiques, les deux forces sont deux poids :
- le poids de l’objet que l’on cherche à peser ;
- le poids de masses marquées, dont la masse est connue.
Quand la balance est à l’équilibre, alors l’objet dont on cherche la masse possède la même masse que la somme des masses marquées.
Avec une balance de Kibble, ce sont toujours deux forces qui sont mesurées, mais celle des masses marquées est remplacée par la force magnétique d’un électroaimant. Quand on place la masse inconnue sur la balance, cette dernière penche d’un côté. On fait alors passer un courant électrique dans l’électroaimant : le champ magnétique induit tire alors la balance du côté de l’électroaimant. En faisant varier l’intensité du courant jusqu’à obtenir un état d’équilibre, on peut retrouver la masse de l’objet que l’on cherche en fonction de l’intensité du courant, grâce à l’induction électromagnétique :
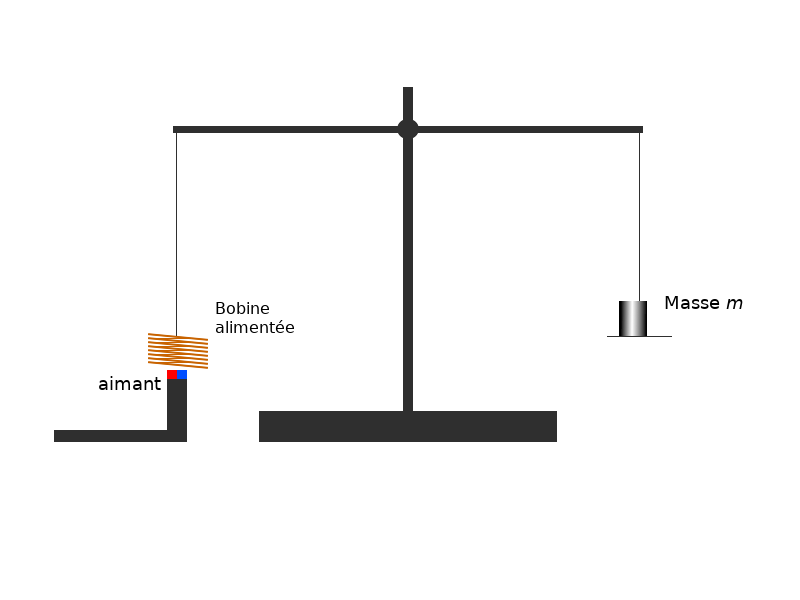
Pour redéfinir le kilogramme, on fonctionne inversement : on va placer le kilogramme étalon sur la balance et on cherchera l’intensité qui équilibre la balance. À ce moment là, on saura quelle intensité permet d’obtenir un kilogramme de force sur la balance.
Mathématiquement, quand la balance est à l’équilibre, il y a une égalité entre le poids $P = mg$ et la force magnétique de la bobine $F = BLI$ :
$$m_kg = BLI$$
Soit, la masse du kilogramme exprimée :
$$m_k = \frac{BLI}{g}$$
Ceci est la version simplifiée, et en pratique, c’est plus compliqué.
La force de l’électroaimant dépend de plusieurs facteurs : de l’intensité du courant, bien-sûr, mais aussi de la longueur totale de fil dans la bobine et l’intensité du champ magnétique de l’aimant permanent. La mesure de ces deux dernière grandeurs est entachée d’incertitudes, mais on peut éliminer le besoin de les mesurer, à l’aide d’une seconde étape.
La seconde étape est de faire descendre l’électroaimant avec une vitesse connue au dessus de l’aimant. L’aimant va induire un courant dans la bobine et l’on va mesurer la tension électrique à ses bornes.
L’expression de la tension $U$ dépend de la vitesse de descente $v$, du champ magnétique $B$ et la longueur de la bobine $L$ :
$$U = vBL$$
En combinant cet équation avec la précédente, on obtient une expression de la masse indépendante de l’aimant et de la longueur de la bobine :
$$m_k = \frac{UI}{gv}$$
Il reste à mesurer l’intensité $I$ et la tension $U$ : une méthode ultra-précise est d’utiliser des composants à comportement quantique.
La tension $U$ peut être déterminée par une jonction de Josephson. Il s’agit de deux matériaux supraconducteurs séparés par de très fins isolants. Cette jonction voit apparaître une tension $U'$ quand elle est soumise à un champ électromagnétique :
$$U' = h\left(\frac{nf}{2e}\right)$$
Où :
- $h$ est la constante de Planck
- $n$ le nombre de jonction de Josephson empilés (donc mises en série)
- $f$ la fréquence du champ électromagnétique
- $e$ est la charge élémentaire.
En ajustant la fréquence, on peut égaliser la tension aux borne des jonctions avec la tension induite par l’aimant sur la bobine. On a alors $U' = U$.
L’intensité $I$ peut être mesurée par une simple loi d’Ohm. Donc plutôt que de mesurer l’intensité $I$, on va mesurer une tension et une résistance : $I = \frac{U}{R}$.
La tension $U$ est à nouveau mesurée par effet Josephson. Quant à la résistance $R$, elle est déterminée par effet Hall quantique (version quantique de l’effet Hall, qui est l’apparition d’une tension perpendiculaire au sens de passage d’un courant dans un conducteur, à cause de la réponse des charges électriques de ce conducteur au champ magnétique induit par ce courant) :
$$R = \frac{1}{p}\frac{h}{e^2}$$
Où :
- $p$ est une constante connue dépendant de la balance
- $h$ la constante de Planck
- $e$ est la charge élémentaire
En prenant ces différentes équations, en replaçant les différentes variables successives et en réarrangeant les différents termes, on obtient une expression de la constante de Planck en fonction du kilogramme étalon :
$$h =\left(\frac{4}{pn^2} \frac{gv}{f^2}\right)m_k$$
$p$, $n$, $f$ sont connus.
$g$, $v$ sont mesurées (par interférométrie laser).
La masse $m_k$ est par définition de 1 kg. On vient donc de déterminer la constante de Planck à partir du kilogramme étalon.
Maintenant, on fixe la constante de Planck (cette valeur devient alors sa valeur définitive) et l’on peut exprimer le kilogramme en fonction de la constante de Planck :
$$m = h\left(\frac{f^2}{gv}\frac{pn^2}{4}\right)$$
Du coup on y est : on peut exprimer le kilogramme sur la balance en fonction de constantes physiques et de quelques instruments de mesures tous indépendants de la masse (vu que c’est ce qu’on l’on cherche) !
À partir de maintenant, on n’a plus besoin de l’étalon du kilogramme. Si l’on désire savoir combien pèse un objet, on le met sur la balance, on effectue les mesures et c’est la valeur de la constante de Planck qu’on utiliser dans les calculs pour déterminer la masse. C’est la constante de Planck qui devient la référence et qui permet de calculer n’importe quelle masse.
La nouvelle définition du kilogramme
Avant, le kilogramme était défini comme la valeur de la masse du prototype international du kilogramme, stocké à Paris. La nouvelle définition proposée et qui devrait être accepté par le CGPM est :
Le kilogramme, kg, est l'unité de masse ; sa valeur est définie en fixant la valeur numérique de la constante de Planck à exactement 6,626 06 ×10⁻³⁴ quand elle est exprimée en s⁻¹⋅m²⋅kg, ce qui correspond à des J⋅s.
Ce qui, il faut l’avouer, est une définition davantage mathématique que littéraire. D’ailleurs, les définitions officielles de toutes les unités sont modifiées pour suivre le même schéma, marquant l’emphase sur le fait que l’unité dépend de la constante physique.
Tout ce qui reste à faire si l’on veut étalonner une masse, c’est utiliser une balance de Kibble, faire ses mesures et prendre la valeur de 6,626 06 ×10⁻³⁴ pour la constante de Planck. Ce qui est plus rapidement dit que fait…
Quelques limites à cette nouvelle approche
On peut s’en douter à lire cet article : autant un étalon en platine est un objet simple, autant une balance de Kibble est un objet très complexe.
Il faut des composants à la pointe de la technologie, être dans une région sans influence extérieure (radio, magnétique et même des séismes !) et il faut même aller jusqu’à cartographier l’accélération de la pesanteur de la pièce où se trouve la balance.
À tel point, d’ailleurs, que seuls certains pays disposent de la technologie pour les fabriquer et les opérer. D’un point de vu politique et social, ceci peut également être une source de problèmes.
Sur le plan technique, il existe la difficulté d’opérer un tel protocole de mesure : la précision des mesures est telle que deux masses qu’on supposerait identique mais en métaux différents seront vue différemment par la balance ! En effet, le métal le moins dense occupera un volume plus important et son centre de masse sera un peu plus haut. Ceci implique une différence dans la valeur du champ de pesanteur (chose que je mets en évidence dans mon article sur le kilo de plumes et le kilo de plomb).